普物二总结——电学部分# Chap 32/33 The Steady Magnetic Field# 32-1 Basic phenomena# history
first hard disk 1957:50 platters
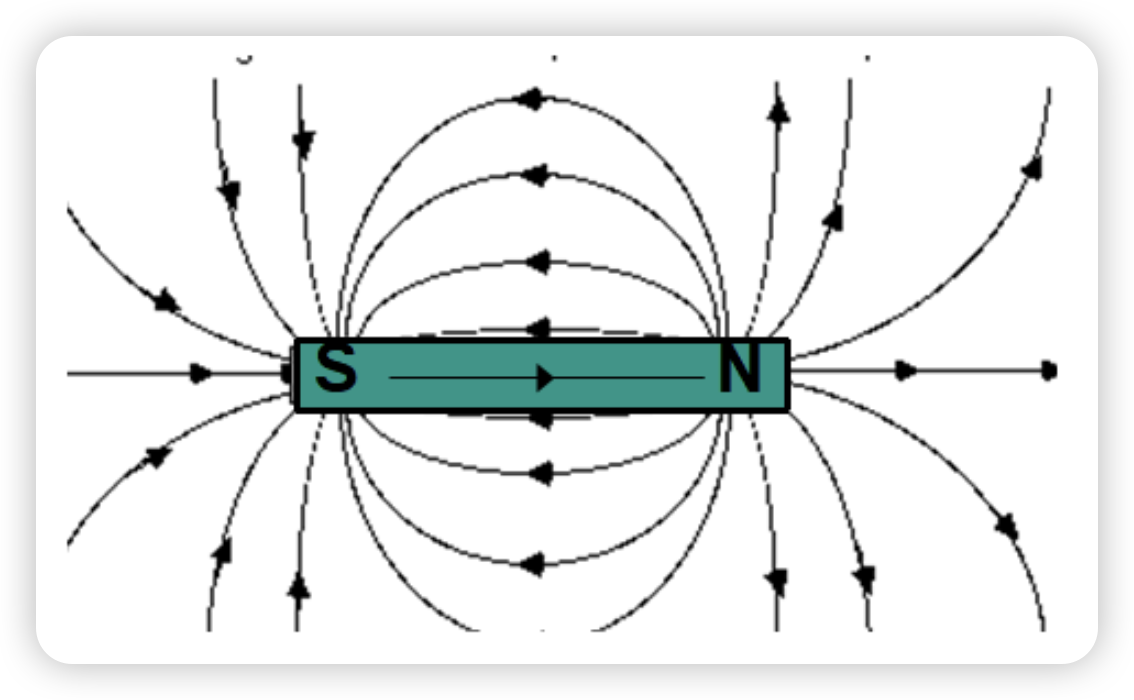
Basic Phenomena of Magnetism# attract small bits of metal have two poles like poles repel, and unlike poles attract oersted experiment: B , i → F B,i\to F B , i → F Solenoid is similar to a bar magnet Interaction between electric currents
the magnetic field line distribution is like electric field of a electdipole pair.
Magnetic Monopoles# since no monopole has ever been found ∮ B ⃗ ⋅ d A ⃗ = 0 \displaystyle \oint \vec B\cdot \mathrm d \vec A=0 ∮ B ⋅ d A = 0
Magnetic field# (Ampere) molecular current: he bind solenoid and a magnet
electric charge in motion is the source of Magnetic Fields
Ampere’s Law(1820.12.4)# Ampere’s Law
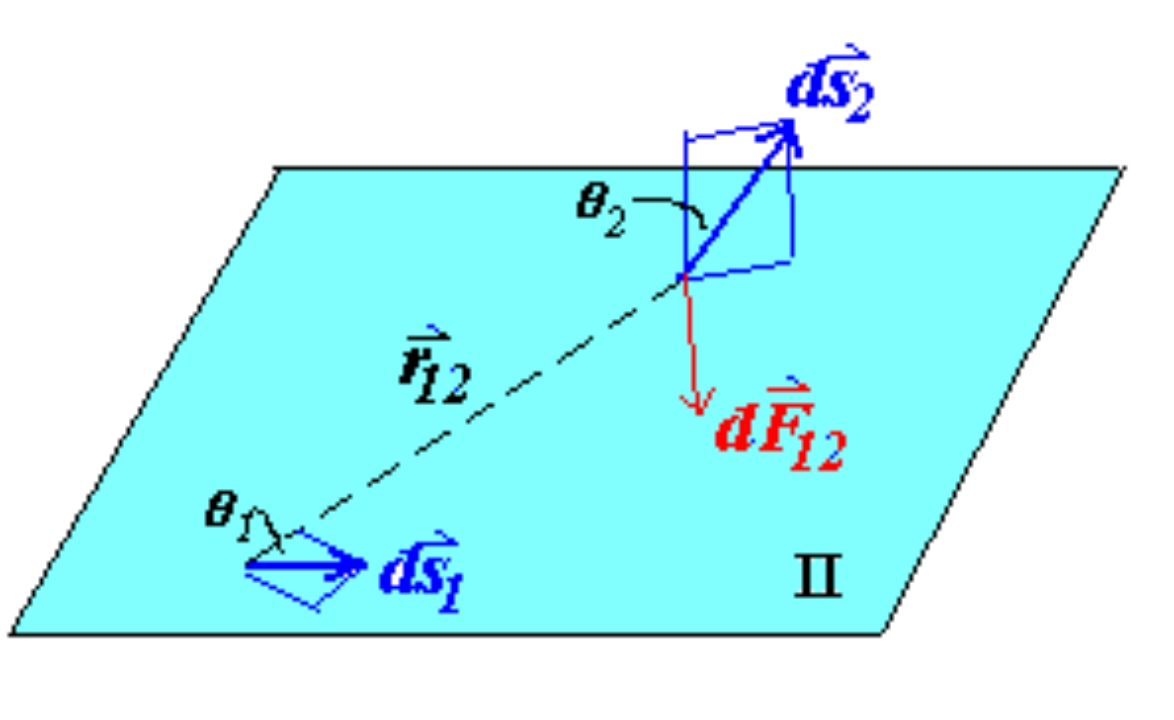
Current element i d s ⃗ i\mathrm d \vec s i d s d F 12 ∝ i 1 i 2 d s 1 d s 2 r 12 2 = μ 0 4 π ⋅ i 2 d s ⃗ 2 × ( i 1 d s ⃗ 1 × r ^ 12 ) r 12 2 \mathrm d F_{12}\propto \frac{i_1i_2\mathrm d s_1\mathrm d s_2}{r_{12}^2}=\frac{\mu _0}{4\pi } \cdot \frac{i_2\mathrm d \vec s_2\times (i_1\mathrm d \vec s_1\times \hat r_{12})}{r_{12}^2} d F 12 ∝ r 12 2 i 1 i 2 d s 1 d s 2 = 4 π μ 0 ⋅ r 12 2 i 2 d s 2 × ( i 1 d s 1 × r ^ 12 ) μ 0 = 4 π × 1 0 − 7 ( N ⋅ A − 2 ) \mu_0 =4\pi\times10^{-7}(N\cdot A^{-2}) μ 0 = 4 π × 1 0 − 7 ( N ⋅ A − 2 )
the consider two examples
eg1
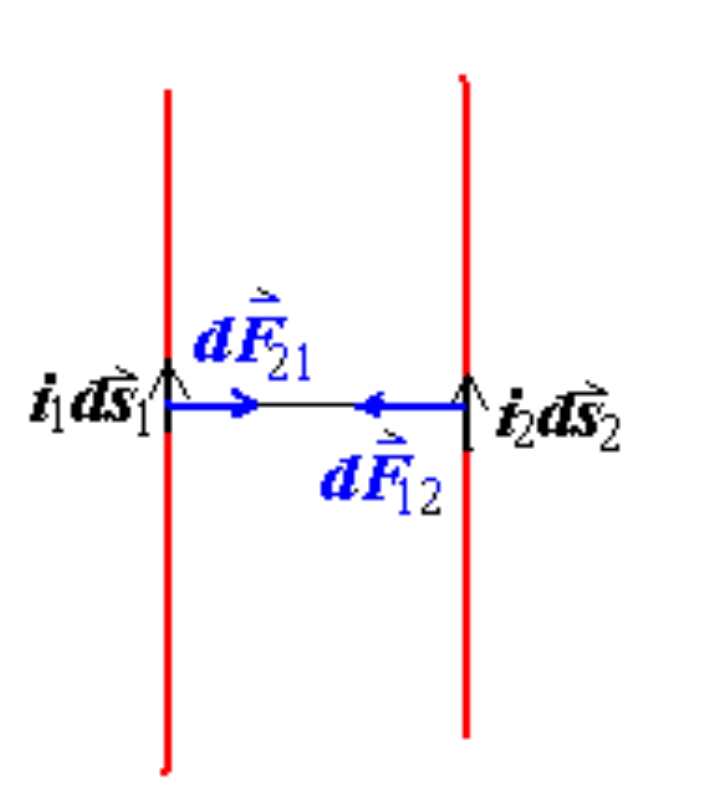
d F ⃗ 12 = μ 0 4 π i 2 d s ⃗ 2 × ( i 1 d s ⃗ 1 × r ^ 12 ) r 12 2 d s ⃗ 1 ⊥ r ^ 12 ∴ d F 12 = μ 0 4 π i 1 i 2 d s 1 d s 2 r 12 2 d F ⃗ 21 = μ 0 4 π i 1 d s ⃗ 1 × ( i 2 d s ⃗ 2 × r ^ 21 ) r 21 2 d s ⃗ 2 ⊥ r ^ 21 ∴ d F 21 = μ 0 4 π i 1 i 2 d s 1 d s 2 r 12 2 d F 12 = d F 21 \begin{aligned} &d\vec{F}_{12}=\frac{\mu_0}{4\pi}\frac{i_2d\vec{s}_2\times(i_1d\vec{s}_1\times\hat{r}_{12})}{r_{12}^2} \\ &d\vec{s}_1\perp\hat{r}_{12} \\ &\therefore dF_{12}=\frac{\mu_0}{4\pi}\frac{i_1i_2ds_1ds_2}{r_{12}^2}\\&d\vec{F}_{21}=\frac{\mu_0}{4\pi}\frac{i_1d\vec{s}_1\times(i_2d\vec{s}_2\times\hat{r}_{21})}{r_{21}^2}\\&d\vec{s}_2\perp\hat{r}_{21}\\&\therefore dF_{21}=\frac{\mu_0}{4\pi}\frac{i_1i_2ds_1ds_2}{r_{12}^2}\\&\mathrm d F_{12}= \mathrm d F_{21}\end{aligned} d F 12 = 4 π μ 0 r 12 2 i 2 d s 2 × ( i 1 d s 1 × r ^ 12 ) d s 1 ⊥ r ^ 12 ∴ d F 12 = 4 π μ 0 r 12 2 i 1 i 2 d s 1 d s 2 d F 21 = 4 π μ 0 r 21 2 i 1 d s 1 × ( i 2 d s 2 × r ^ 21 ) d s 2 ⊥ r ^ 21 ∴ d F 21 = 4 π μ 0 r 12 2 i 1 i 2 d s 1 d s 2 d F 12 = d F 21
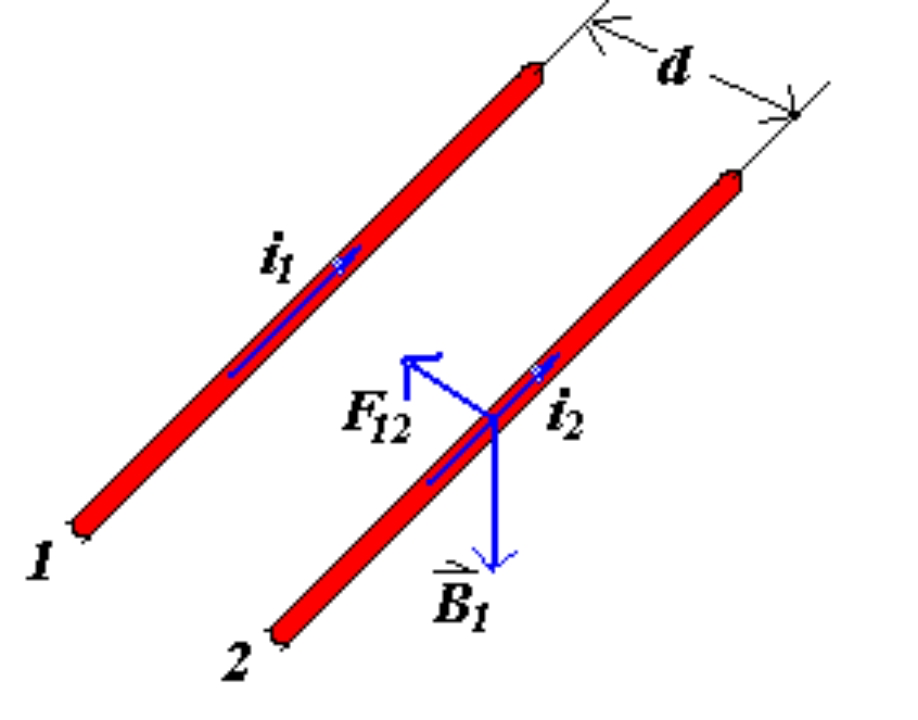
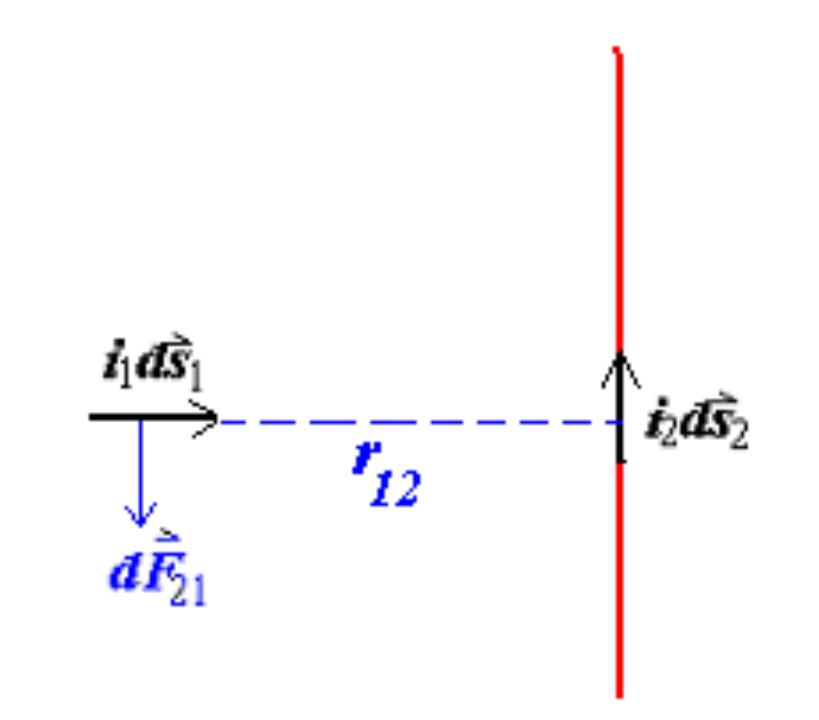
d F 12 = 0 d F 21 = μ 0 4 π i 1 i 2 d s 1 d s 2 r 12 2 \mathrm d F_{12}=0\\\mathrm d F_{21}=\frac{\mu_0}{4\pi}\frac{i_1i_2\mathrm d s_1\mathrm d s_2}{r_{12}^2} d F 12 = 0 d F 21 = 4 π μ 0 r 12 2 i 1 i 2 d s 1 d s 2 The Magnetic Induction Strength# F ⃗ 12 = 1 4 π ε 0 q 1 q 2 r 12 2 r ^ 12 F ⃗ 12 = q 2 E ⃗ 1 , E ⃗ 1 = F ⃗ 12 q 2 ∴ E ⃗ 1 = 1 4 π ε 0 q 1 r 12 2 r ^ 12 \vec{F}_{12}=\frac1{4\pi\varepsilon_0}\frac{q_1q_2}{r_{12}^2}\hat{r}_{12}\\\vec{F}_{12}=q_2\vec{E}_1, \vec{E}_1=\frac{\vec{F}_{12}}{q_2}\\\therefore\vec{E}_1=\frac1{4\pi\varepsilon_0}\frac{q_1}{r_{12}^2}\hat{r}_{12} F 12 = 4 π ε 0 1 r 12 2 q 1 q 2 r ^ 12 F 12 = q 2 E 1 , E 1 = q 2 F 12 ∴ E 1 = 4 π ε 0 1 r 12 2 q 1 r ^ 12 Ampere’s Law d F ⃗ 12 = μ 0 4 π i 2 d s ⃗ 2 × ( i 1 d s ⃗ 1 × r ^ 12 ) r 12 2 d\vec{F}_{12}=\frac{\mu_0}{4\pi}\frac{i_2d\vec{s}_2\times(i_1d\vec{s}_1\times\hat{r}_{12})}{r_{12}^2} d F 12 = 4 π μ 0 r 12 2 i 2 d s 2 × ( i 1 d s 1 × r ^ 12 ) let us call i 2 d s ⃗ 2 i_2\mathrm d \vec s_2 i 2 d s 2
d F ⃗ 2 = i 2 d s ⃗ 2 × μ 0 4 π ∮ L 1 i 1 d s ⃗ 1 × r ^ 12 r 12 2 Define: B ⃗ 1 = μ 0 4 π ∮ L 1 i 1 d s ⃗ 1 × r ^ 12 r 12 2 ∴ d F ⃗ 2 = i 2 d s ⃗ 2 × B ⃗ 1 \begin{aligned}&d\vec{F}_2=i_2d\vec{s}_2\times\frac{\mu_0}{4\pi}\oint_{\mathrm{L}_1}\frac{i_1d\vec{s}_1\times\hat{r}_{12}}{r_{12}^2}\\&\text{Define:}\quad\vec{B}_1=\frac{\mu_0}{4\pi}\oint_{\mathrm{L}_1}\frac{i_1d\vec{s}_1\times\hat{r}_{12}}{r_{12}^2}\\&\therefore\quad d\vec{F}_2=i_2d\vec{s}_2\times\vec{B}_1\end{aligned} d F 2 = i 2 d s 2 × 4 π μ 0 ∮ L 1 r 12 2 i 1 d s 1 × r ^ 12 Define: B 1 = 4 π μ 0 ∮ L 1 r 12 2 i 1 d s 1 × r ^ 12 ∴ d F 2 = i 2 d s 2 × B 1 d F ⃗ 2 = i 2 d s ⃗ 2 × B ⃗ 1 d F 2 = i 2 d s 2 B 1 sin θ θ = 0 , d F 2 = 0 θ = π 2 , d F 2 m a x i m u n Define: B 1 = ( d F 2 ) max i 2 d s 2 ⇒ B ⃗ 1 = μ 0 4 π ∮ L 1 i 1 d s ⃗ 1 × r ^ 12 r 12 2 \begin{aligned} &d\vec{F}_2=i_2d\vec{s}_2\times\vec{B}_1 \\ &dF_2=i_2ds_2B_1\sin\theta \\ &\theta=0,dF_2=0 \\ &\theta=\frac{\pi}{2}, dF_{2} \mathrm{maximun} \\ &\boxed{\textbf{Define: }B_1=\frac{\left(dF_2\right)_{\max}}{i_2ds_2}} \\&\Rightarrow \vec B_1=\frac{\mu_0}{4\pi} \oint_{L_1} \frac{i_1\mathrm d \vec s_1 \times \hat r_{12}}{r_{12}^2} \end{aligned} d F 2 = i 2 d s 2 × B 1 d F 2 = i 2 d s 2 B 1 sin θ θ = 0 , d F 2 = 0 θ = 2 π , d F 2 maximun Define: B 1 = i 2 d s 2 ( d F 2 ) m a x ⇒ B 1 = 4 π μ 0 ∮ L 1 r 12 2 i 1 d s 1 × r ^ 12 the Unit T T T 1 N / ( m ⋅ A ) = 1 0 4 G a u s s 1N/(m\cdot A)=10^4 \mathrm{~Gauss} 1 N / ( m ⋅ A ) = 1 0 4 Gauss
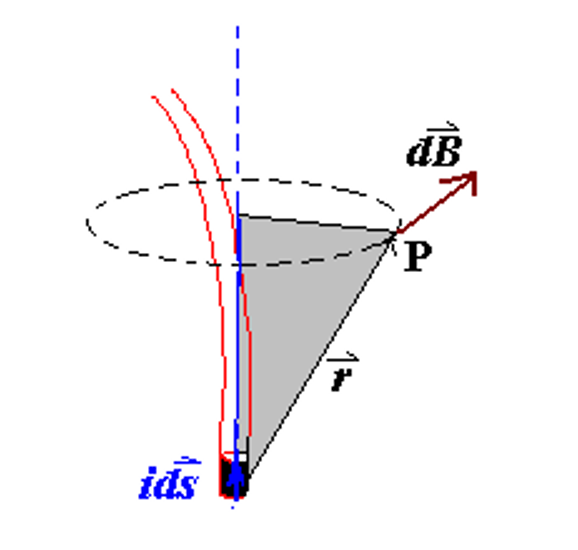
32-2 The magneticn field of a Current-Carrying loop# Biot-Savart Law
B ⃗ = μ 0 4 π ∮ L i d s ⃗ × r ^ r 2 \vec{B}=\frac{\mu_0}{4\pi}\oint_L\frac{id\vec{s}\times\hat{r}}{r^2} B = 4 π μ 0 ∮ L r 2 i d s × r ^
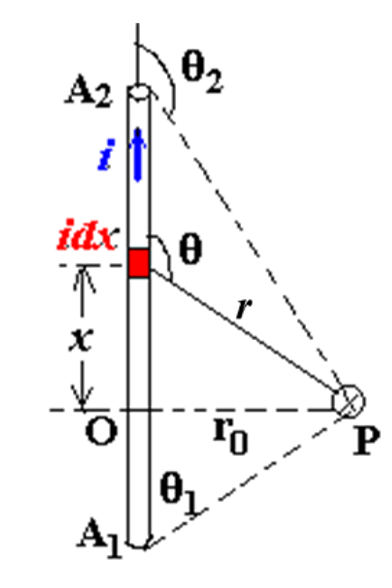
B = ∫ A 1 A 2 d B = μ 0 4 π ∫ A 1 A 2 i sin θ d x r 2 r 0 = r sin ( π − θ ) = r sin θ , r = r 0 sin θ x = − r 0 c t g θ , d x = r 0 d θ sin 2 θ B = ∫ θ 1 θ 2 μ 0 i 4 π sin θ ⋅ r 0 d θ sin 2 θ r 0 2 = μ 0 i 4 π r 0 ∫ θ 1 θ 2 sin θ d θ = μ 0 i 4 π r 0 ( cos θ 1 − cos θ 2 ) = μ 0 i 2 π r 0 ∝ 1 r 0 \begin{aligned}&B=\int_{A_{1}}^{A_{2}}dB=\frac{\mu_{0}}{4\pi}\int_{A_{1}}^{A_{2}}\frac{i\sin\theta dx}{r^{2}}\\&r_{0}=r\sin(\pi-\theta)=r\sin\theta, r=\frac{r_{0}}{\sin\theta}\\&x=-r_{0}ctg\theta,\quad dx=\frac{r_{0}d\theta}{\sin^{2}\theta}\\&B=\int_{\theta_{1}}^{\theta_{2}}\frac{\mu_{0}i}{4\pi}\frac{\sin\theta\cdot\frac{r_{0}d\theta}{\sin^{2}\theta}}{r_{0}^{2}}=\frac{\mu_{0}i}{4\pi r_{0}}\int_{\theta_{1}}^{\theta_{2}}\sin\theta d\theta\\&=\frac{\mu_{0}i}{4\pi r_{0}}(\cos\theta_{1}-\cos\theta_{2})\\&=\frac{\mu _0i}{2\pi r_0}\propto \frac{1}{r_0}\end{aligned} B = ∫ A 1 A 2 d B = 4 π μ 0 ∫ A 1 A 2 r 2 i sin θ d x r 0 = r sin ( π − θ ) = r sin θ , r = sin θ r 0 x = − r 0 c t g θ , d x = sin 2 θ r 0 d θ B = ∫ θ 1 θ 2 4 π μ 0 i r 0 2 sin θ ⋅ s i n 2 θ r 0 d θ = 4 π r 0 μ 0 i ∫ θ 1 θ 2 sin θ d θ = 4 π r 0 μ 0 i ( cos θ 1 − cos θ 2 ) = 2 π r 0 μ 0 i ∝ r 0 1
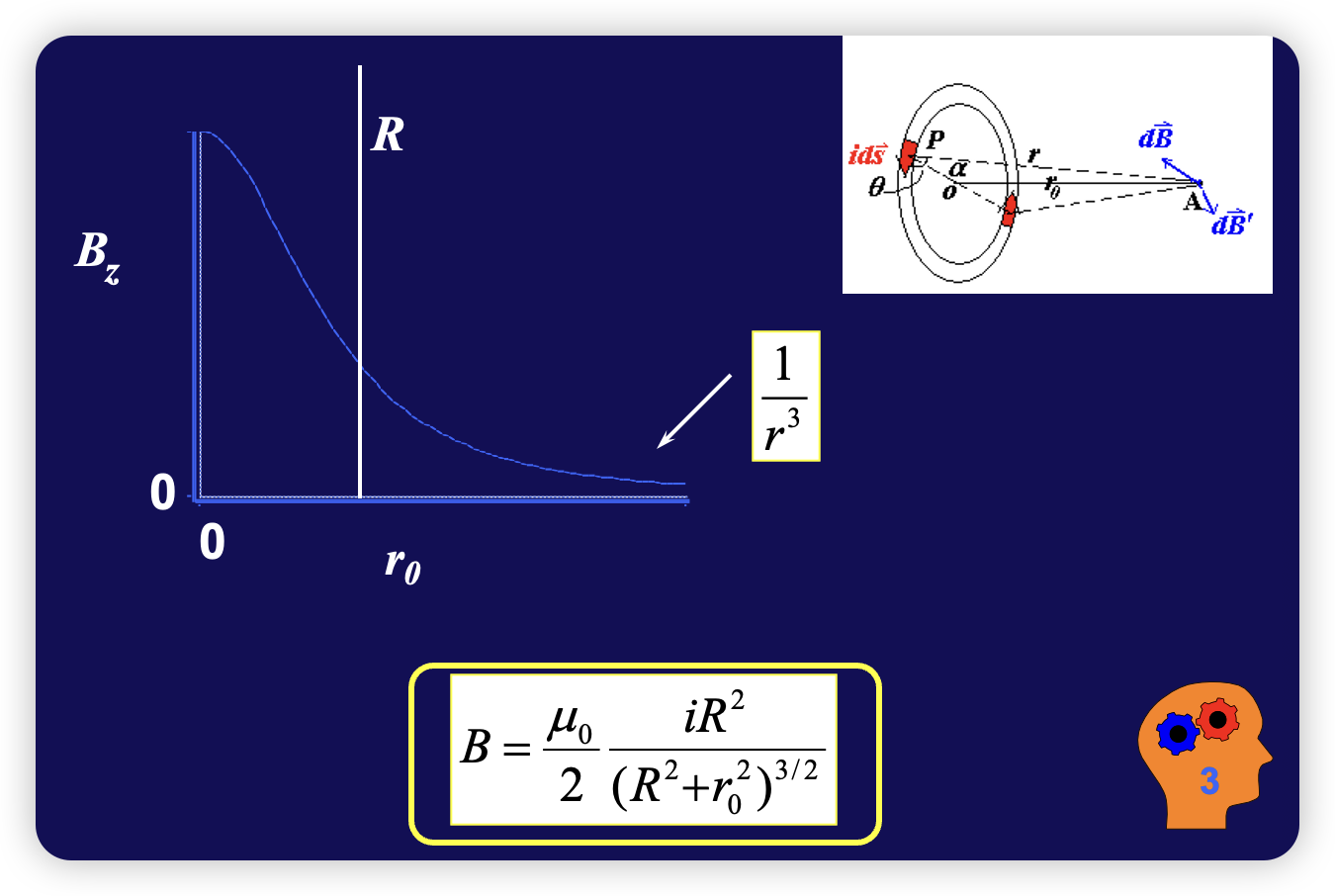
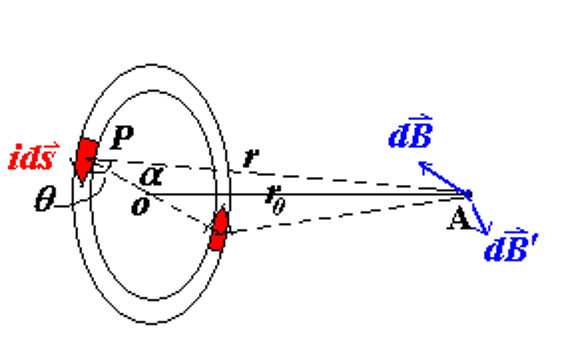
∣ d B ⃗ ∣ = ∣ d B ⃗ ′ ∣ d B ⃗ = μ 0 4 π i d s ⃗ × r ^ r 2 d B x = d B ⋅ cos α d B = μ 0 4 π i d s r 2 sin θ θ = π 2 , sin θ = 1 , r = r 0 / sin α B x = ∫ d B cos α B = μ 0 i 4 π ∮ sin 2 α r 0 2 cos α d s = μ 0 i 4 π r 0 2 sin 2 α cos α ⋅ 2 π R B = μ 0 2 i R 2 ( R 2 + r 0 2 ) 3 2 → r 0 = 0 B = μ 0 i 2 R → r 0 > > R B = μ 0 i R 2 2 r 0 3 \begin{aligned} &\left|d\vec{B}\right|=\left|d\vec{B}^{\prime}\right| \\ &d{\vec{B}}={\frac{\mu_{0}}{4\pi}}{\frac{id{\vec{s}}\times{\hat{r}}}{r^{2}}} \\ &dB_{x}=dB\cdot\cos\alpha \\ &dB=\frac{\mu_{0}}{4\pi}\frac{ids}{r^{2}}\sin\theta \\ &\theta=\frac{\pi}{2}, \sin\theta=1, r=r_{0}/\sin\alpha \\ &B_{x}=\int dB\cos\alpha \\ &B=\frac{\mu_{0}i}{4\pi}\oint\frac{\sin^{2}\alpha}{r_{0}^{2}}\cos\alpha ds\\&=\frac{\mu_{0}i}{4\pi r_{0}^{2}}\sin^{2}\alpha\cos\alpha\cdot2\pi R\\ &B=\frac{\mu_0}{2} \frac{iR^2}{(R^2+r_0^2)^{\frac{3}{2}}}\xrightarrow{r_0=0}B=\frac{\mu_0 i}{2R}\\\ &\xrightarrow {r_0>>R} B=\frac{\mu_0 i R^2}{2r_0^3} \end{aligned} d B = d B ′ d B = 4 π μ 0 r 2 i d s × r ^ d B x = d B ⋅ cos α d B = 4 π μ 0 r 2 i d s sin θ θ = 2 π , sin θ = 1 , r = r 0 / sin α B x = ∫ d B cos α B = 4 π μ 0 i ∮ r 0 2 sin 2 α cos α d s = 4 π r 0 2 μ 0 i sin 2 α cos α ⋅ 2 π R B = 2 μ 0 ( R 2 + r 0 2 ) 2 3 i R 2 r 0 = 0 B = 2 R μ 0 i r 0 >> R B = 2 r 0 3 μ 0 i R 2 we can define magnetic dipole moment μ \mu μ p ⃗ = q l ⃗ \vec p= q\vec l p = q l
B = μ 0 i R 2 2 r 0 3 = μ 0 i π R 2 2 π r 0 3 = μ 0 i A 2 π r 0 3 Define: μ = i A = i π R 2 ( μ ⃗ = i A ⃗ ) B = μ 0 2 i R 2 r 0 3 = μ 0 2 π i π R 2 r 0 3 = μ 0 2 π μ r 0 3 B=\frac{\mu_0iR^2}{2r_0^3}=\frac{\mu_0i\pi R^2}{2\pi r_0^3}=\frac{\mu_0iA}{2\pi r_0^3}\\\begin{aligned}&\text{Define: }\mu=iA=i\pi R^2(\vec \mu =i\vec A)\\&B=\frac{\mu_{0}}{2}\frac{iR^{2}}{r_{0}^{3}}=\frac{\mu_{0}}{2\pi}\frac{i\pi R^{2}}{r_{0}^{3}}=\frac{\mu_{0}}{2\pi}\frac{\mu}{r_{0}^{3}}\end{aligned} B = 2 r 0 3 μ 0 i R 2 = 2 π r 0 3 μ 0 iπ R 2 = 2 π r 0 3 μ 0 i A Define: μ = i A = iπ R 2 ( μ = i A ) B = 2 μ 0 r 0 3 i R 2 = 2 π μ 0 r 0 3 iπ R 2 = 2 π μ 0 r 0 3 μ
p757 sample33-5
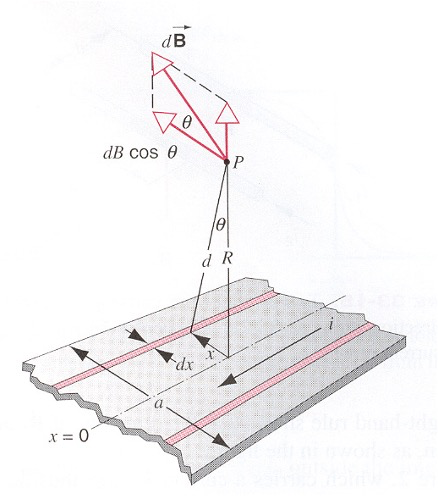
d B = μ 0 d i 2 π d = μ 0 i a d x 2 π d d = R cos θ ⇒ B x = ∫ d B cos θ = μ 0 i 2 π a R ∫ cos 2 θ d x \mathrm d B=\frac{\mu _0 di}{2\pi d}=\frac{\mu _0 \frac{i}{a} dx}{2\pi d}\\ d=\frac{R}{\cos \theta }\Rightarrow B_x=\int dB\cos \theta=\frac{\mu_0i}{2\pi a R}\int \cos^2\theta dx d B = 2 π d μ 0 d i = 2 π d μ 0 a i d x d = cos θ R ⇒ B x = ∫ d B cos θ = 2 πa R μ 0 i ∫ cos 2 θ d x then
d x = d ( R tan θ ) = R d cos 2 θ dx=\mathrm d (R\tan \theta)=R\frac{\mathrm d}{\cos^2\theta } d x = d ( R tan θ ) = R c o s 2 θ d
B x = μ 0 i 2 π a ∫ − θ θ d θ = μ 0 i π a α = μ 0 i π a arctan a 2 R B_x=\frac{\mu_0 i}{2\pi a}\int_{-\theta}^{\theta}d\theta =\frac{\mu _0 i}{\pi a}\alpha =\frac{\mu_0 i}{\pi a}\arctan \frac{a}{2R} B x = 2 πa μ 0 i ∫ − θ θ d θ = πa μ 0 i α = πa μ 0 i arctan 2 R a R > > a : ( α → tan α ) B = μ 0 i 2 π R R>>a:(\alpha \to \tan \alpha)B=\frac{\mu_0 i}{2\pi R} R >> a : ( α → tan α ) B = 2 π R μ 0 i
R → 0 , B = μ 0 i 2 a R\to 0,B=\frac{\mu_0i}{2a} R → 0 , B = 2 a μ 0 i
Bohr model of the hydrogen atom
a 0 = 0.529 A = 5.29 × 1 0 − 11 m ν = 6.63 × 1 0 15 H z i = e ν = 1.60 × 1 0 − 19 × 6.63 × 1 0 15 = 1.63 × 1 0 − 3 A B = μ 0 i 2 R = 4 π × 1 0 − 7 × 1.06 × 1 0 − 3 2 × 5.29 × 1 0 − 11 = 12.6 T μ B = i A = 1.63 × 1 0 − 3 × π × ( 5.29 × 1 0 − 11 ) 2 = 0.923 × 1 0 − 23 A ⋅ m 2 \begin{aligned}&a_0=0.529A=5.29\times10^{-11}m\\&\nu=6.63\times10^{15}Hz\\&i=e\nu=1.60\times10^{-19}\times6.63\times10^{15}=1.63\times10^{-3}A\\&B=\frac{\mu_0i}{2R}=\frac{4\pi\times10^{-7}\times1.06\times10^{-3}}{2\times5.29\times10^{-11}}=12.6T\\&\mu_\mathrm{B}=iA=1.63\times10^{-3}\times\pi\times(5.29\times10^{-11})^2\\&=0.923\times10^{-23}A\cdot m^2\end{aligned} a 0 = 0.529 A = 5.29 × 1 0 − 11 m ν = 6.63 × 1 0 15 Hz i = e ν = 1.60 × 1 0 − 19 × 6.63 × 1 0 15 = 1.63 × 1 0 − 3 A B = 2 R μ 0 i = 2 × 5.29 × 1 0 − 11 4 π × 1 0 − 7 × 1.06 × 1 0 − 3 = 12.6 T μ B = i A = 1.63 × 1 0 − 3 × π × ( 5.29 × 1 0 − 11 ) 2 = 0.923 × 1 0 − 23 A ⋅ m 2 called as Bohr Magnon
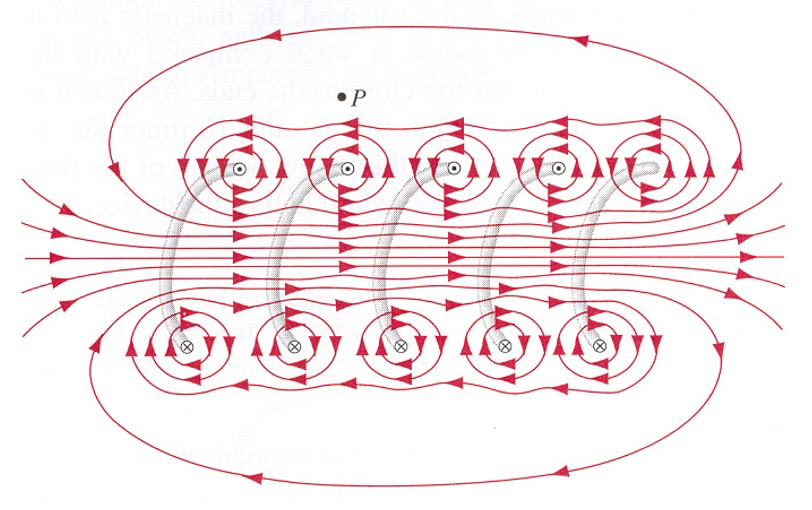
B of Solenoid# Solenoid
A constant magnetic field can (in principle) be produced by an ∞ \infty ∞
Parameters:i , n , R , L i,n,R,L i , n , R , L R < < L R<<L R << L
for a circular loop
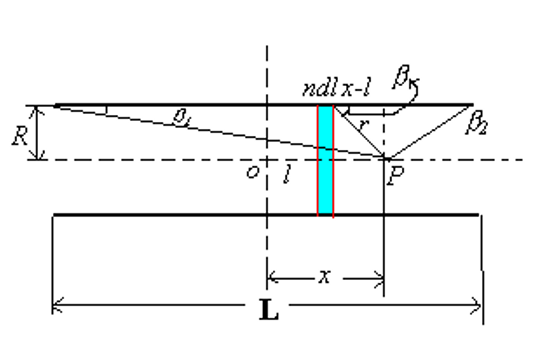
B = μ 0 2 i R 2 ( R 2 + r 0 2 ) 3 / 2 B=\frac{\mu_0}{2}\frac{iR^2}{\left(R^2+r_0^2\right)^{3/2}} B = 2 μ 0 ( R 2 + r 0 2 ) 3/2 i R 2 d B = μ 0 2 R 2 i n d l [ R 2 + ( x − l ) 2 ] 3 / 2 B = μ 0 2 ∫ − L / 2 L / 2 R 2 i n d l [ R 2 + ( x − l ) 2 ] 3 / 2 r = R 2 + ( x − l ) 2 = R sin β x − l R = c t g β ⇒ d l = R sin 2 β d β \begin{aligned} &dB=\frac{\mu_{0}}{2}\frac{R^{2}indl}{\left[R^{2}+(x-l)^{2}\right]^{3/2}} \\ &B=\frac{\mu_{0}}{2}\int_{-L/2}^{L/2}\frac{R^{2}indl}{\left[R^{2}+\left(x-l\right)^{2}\right]^{3/2}} \\ &r={\sqrt{R^{2}+\left(x-l\right)^{2}}}={\frac{R}{\sin\beta}} \\ &\frac{x-l}{R}=ctg\beta\Rightarrow dl=\frac{R}{\sin^{2}\beta}d\beta \end{aligned} d B = 2 μ 0 [ R 2 + ( x − l ) 2 ] 3/2 R 2 in d l B = 2 μ 0 ∫ − L /2 L /2 [ R 2 + ( x − l ) 2 ] 3/2 R 2 in d l r = R 2 + ( x − l ) 2 = sin β R R x − l = c t g β ⇒ d l = sin 2 β R d β then
B = μ 0 2 ∫ β 1 β 2 R 2 n i R sin 2 β d β ( R 2 sin 2 β ) 3 / 2 = μ 0 2 ⋅ n i ∫ β 1 β 2 sin β d β = 1 2 μ 0 n i ( cos β 1 − cos β 2 ) \begin{aligned} &B=\frac{\mu_{0}}{2}\int_{\beta_{1}}^{\beta_{2}}\frac{R^{2}ni\frac{R}{\sin^{2}\beta}d\beta}{(\frac{R^{2}}{\sin^{2}\beta})^{3/2}} \\ &=\frac{\mu_{0}}{2}\cdot ni\int_{\beta_{1}}^{\beta_{2}}\sin\beta d\beta \\ &=\frac12 \mu_{0}ni(\cos\beta_{1}-\cos\beta_{2}) \end{aligned} B = 2 μ 0 ∫ β 1 β 2 ( s i n 2 β R 2 ) 3/2 R 2 ni s i n 2 β R d β = 2 μ 0 ⋅ ni ∫ β 1 β 2 sin β d β = 2 1 μ 0 ni ( cos β 1 − cos β 2 ) use
cos β 1 = x + L / 2 R 2 + ( x + L / 2 ) 2 cos β 2 = x − L / 2 R 2 + ( x − L / 2 ) 2 \cos\beta_{1}=\frac{x+L/2}{\sqrt{R^{2}+\left(x+L/2\right)^{2}}}\\\cos\beta_{2}=\frac{x-L/2}{\sqrt{R^{2}+\left(x-L/2\right)^{2}}} cos β 1 = R 2 + ( x + L /2 ) 2 x + L /2 cos β 2 = R 2 + ( x − L /2 ) 2 x − L /2 with
L → ∞ , β 1 = 0 , β 2 = π L\to \infty ,\beta _1=0,\beta_2=\pi L → ∞ , β 1 = 0 , β 2 = π
B = 1 2 μ 0 n i ( 1 + 1 ) = μ 0 n i B=\frac{1}{2}\mu _0ni(1+1)=\mu_0ni B = 2 1 μ 0 ni ( 1 + 1 ) = μ 0 ni
β 1 = 0 , β 2 = π 2 \beta _1=0,\beta_2=\frac{\pi}{2} β 1 = 0 , β 2 = 2 π
B = 1 2 μ 0 n i ( 1 − 0 ) = 1 2 μ 0 n i B=\frac{1}{2}\mu_0 n i(1-0)=\frac{1}{2}\mu_0 ni B = 2 1 μ 0 ni ( 1 − 0 ) = 2 1 μ 0 ni
The field outside the ideal solenoid is zero.
eg
B = 1 2 μ 0 n i ( cos β 1 − cos β 2 ) B=\frac12 \mu_{0}ni(\cos\beta_{1}-\cos\beta_{2}) B = 2 1 μ 0 ni ( cos β 1 − cos β 2 ) With this
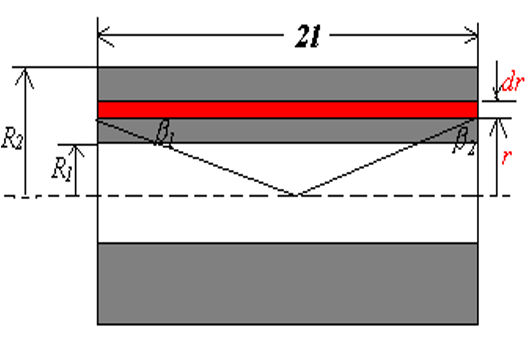
n i = N i L ⇒ j L d r L = j d r = N i 2 l ( R 2 − R 1 ) d r cos β 2 = − cos β 1 , cos β 1 = l l 2 + r 2 \begin{aligned}&ni=\frac{Ni}{L}\Rightarrow\frac{jLdr}{L}=jdr=\frac{Ni}{2l(R_{2}-R_{1})} dr\\&\cos\beta_{2}=-\cos\beta_{1},\cos\beta_{1}=\frac{l}{\sqrt{l^{2}+r^{2}}}\end{aligned} ni = L N i ⇒ L j L d r = j d r = 2 l ( R 2 − R 1 ) N i d r cos β 2 = − cos β 1 , cos β 1 = l 2 + r 2 l d B = 1 2 μ 0 N i 2 l ( R 2 − R 1 ) ⋅ 2 l l 2 + r 2 d r B = μ 0 j l ∫ R 1 R 2 d r l 2 + r 2 = μ 0 j l ln R 2 + R 2 2 + l 2 R 1 + R 1 2 + l 2 \begin{aligned} &dB=\frac{1}{2} \mu_{0} \frac{Ni}{2l(R_{2}-R_{1})}\cdot\frac{2l}{\sqrt{l^{2}+r^{2}}} dr \\ &B=\mu_{0}jl\int_{R_{1}}^{R_{2}}\frac{dr}{\sqrt{l^{2}+r^{2}}} \\ &=\mu_{0}jl\ln\frac{R_{2}+\sqrt{R_{2}^{2}+l^{2}}}{R_{1}+\sqrt{R_{1}^{2}+l^{2}}} \end{aligned} d B = 2 1 μ 0 2 l ( R 2 − R 1 ) N i ⋅ l 2 + r 2 2 l d r B = μ 0 j l ∫ R 1 R 2 l 2 + r 2 d r = μ 0 j l ln R 1 + R 1 2 + l 2 R 2 + R 2 2 + l 2 in practice
we define γ = l R 1 , α = R 2 R 1 \gamma=\frac{l}{R_1},\alpha =\frac{R_2}{R_1} γ = R 1 l , α = R 1 R 2
B 0 = μ 0 h R 1 γ ln α + α 2 + γ 2 1 + 1 + γ 2 B_0=\mu_0hR_1\gamma \ln \frac{\alpha +\sqrt {\alpha^2+\gamma^2}}{1+\sqrt{1+\gamma^2}} B 0 = μ 0 h R 1 γ ln 1 + 1 + γ 2 α + α 2 + γ 2 32-3 Gauss Law and Ampere’s Loop Law for B# let’s first review
for E ⃗ \vec E E
Gauss law:
∮ E ⃗ ∙ d A ⃗ = 1 ε 0 ∑ q , ∇ ∙ E ⃗ = ρ e ε 0 \oint\vec{E}\bullet d\vec{A}=\frac1{\varepsilon_0}\sum q, \nabla\bullet\vec{E}=\frac{\rho_e}{\varepsilon_0} ∮ E ∙ d A = ε 0 1 ∑ q , ∇ ∙ E = ε 0 ρ e Loop law
∮ E ⃗ ∙ d l ⃗ = 0 , ∇ × E ⃗ = 0 ( E ⃗ = − ∇ V ) \oint \vec E\bullet d\vec l =0,\nabla \times \vec E=0(\vec E=-\nabla V) ∮ E ∙ d l = 0 , ∇ × E = 0 ( E = − ∇ V ) Φ B = ∬ B ⃗ ∙ d A ⃗ = ∬ B cos θ d A ( U n i t : T ⋅ m 2 = W b ) \Phi_B=\iint\vec{B}\bullet d\vec{A}=\iint B\cos\theta dA(Unit :T\cdot m^2=Wb) Φ B = ∬ B ∙ d A = ∬ B cos θ d A ( U ni t : T ⋅ m 2 = Wb ) for B ⃗ \vec B B
Gauss law:
∮ B ⃗ ∙ d A ⃗ = 0 , ∇ ∙ B ⃗ = 0 \oint\vec{B}\bullet d\vec{A}=0, \nabla\bullet\vec{B}=0 ∮ B ∙ d A = 0 , ∇ ∙ B = 0 Loop law
∮ B ⃗ ∙ d l ⃗ = μ 0 ∑ i , ∇ × B ⃗ = μ 0 J ⃗ \oint \vec B\bullet d\vec l =\mu _0\sum i,\nabla \times \vec B=\mu_0\vec J ∮ B ∙ d l = μ 0 ∑ i , ∇ × B = μ 0 J fact…
∮ B ⃗ d l ⃗ = μ 0 ∑ i + μ 0 ε 0 d d t ∫ S E ⃗ d S ⃗ \oint \vec B\mathrm d \vec l =\mu_0\sum i+\mu_0\varepsilon_0\frac{\mathrm d}{\mathrm dt}\int _S\vec E\mathrm d \vec S ∮ B d l = μ 0 ∑ i + μ 0 ε 0 d t d ∫ S E d S The differential form is
∇ × B ⃗ = μ 0 J ⃗ + μ 0 ε 0 ∂ E ⃗ ∂ t \nabla \times \vec B =\mu_0\vec J+\mu_0\varepsilon _0\frac{\partial \vec E}{\partial t} ∇ × B = μ 0 J + μ 0 ε 0 ∂ t ∂ E
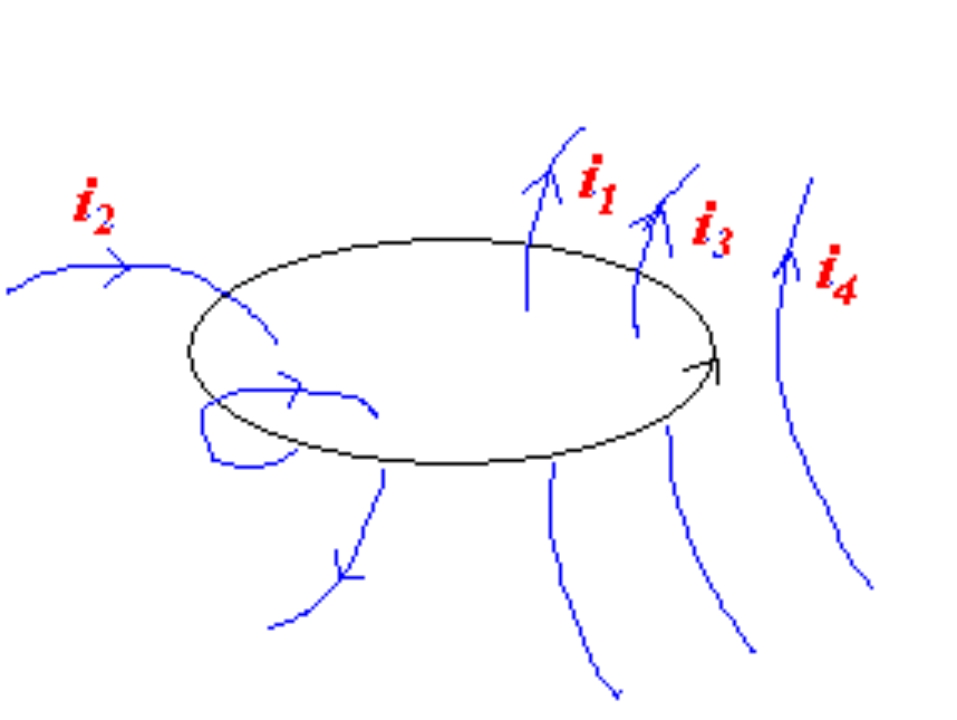
∮ B ⃗ ⋅ d l ⃗ = μ 0 ( i 1 + i 3 − 2 i 2 ) \oint \vec B\cdot \mathrm d\vec l=\mu_0(i_1+i_3-2i_2) ∮ B ⋅ d l = μ 0 ( i 1 + i 3 − 2 i 2 ) egs
[e.g.1]
inf long wire R R R
B ⋅ 2 π r = μ 0 i ⋅ r 2 π R 2 ⇒ B = μ 0 i r 2 π R 2 ( r < R ) ∝ r B\cdot 2\pi r=\mu_0i\cdot \frac{r^2}{\pi R^2}\Rightarrow B=\frac{\mu_0 i r}{2\pi R^2}(r<R)\propto r B ⋅ 2 π r = μ 0 i ⋅ π R 2 r 2 ⇒ B = 2 π R 2 μ 0 i r ( r < R ) ∝ r B ⋅ 2 π r = μ 0 i ⇒ B = μ 0 i 2 π r ( r > R ) ∝ 1 r B\cdot 2\pi r=\mu_0i\Rightarrow B=\frac{\mu_0 i }{2\pi r}(r>R)\propto \frac{1}{r} B ⋅ 2 π r = μ 0 i ⇒ B = 2 π r μ 0 i ( r > R ) ∝ r 1 [e.g.2]
Consider an ∞ \infty ∞ into the screen as shown. Calculate the B field.
for symmetry
we catch a w*w square
∮ B ⃗ ∙ d l ⃗ = 2 B w = μ 0 n w i ⇒ B = 1 2 μ 0 n i \oint \vec B \bullet \mathrm d\vec l=2Bw=\mu_0 n w i\Rightarrow B=\frac{1}{2}\mu_0 ni ∮ B ∙ d l = 2 Bw = μ 0 n w i ⇒ B = 2 1 μ 0 ni [e.g.3]
calculate B for ∞ \infty ∞
view it as two sheets
∮ B ⃗ ∙ d l ⃗ = B w = μ 0 n w i ⇒ B = μ 0 n i \oint \vec B\bullet \mathrm d \vec l =Bw=\mu _0 n w i\Rightarrow B=\mu_0 ni ∮ B ∙ d l = Bw = μ 0 n w i ⇒ B = μ 0 ni [e.g.4]
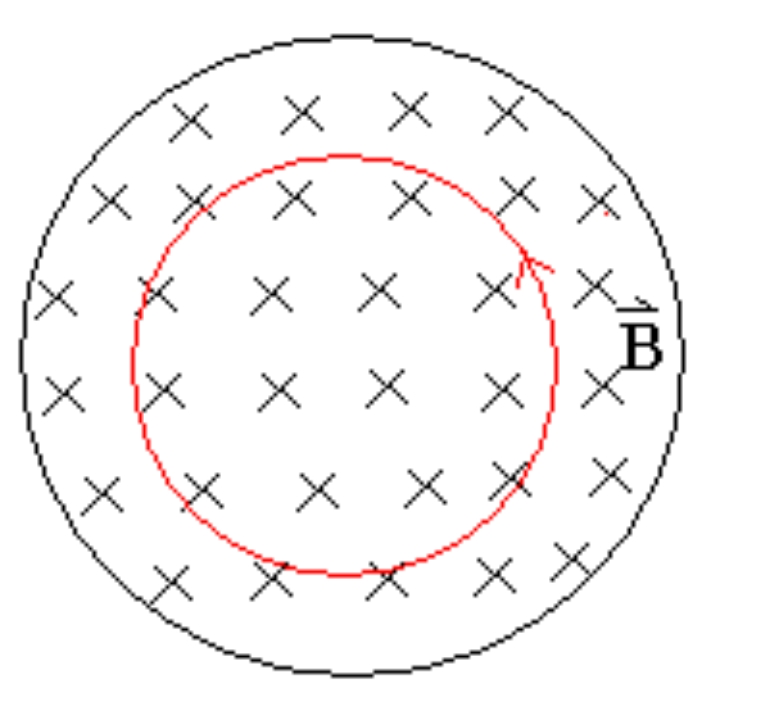
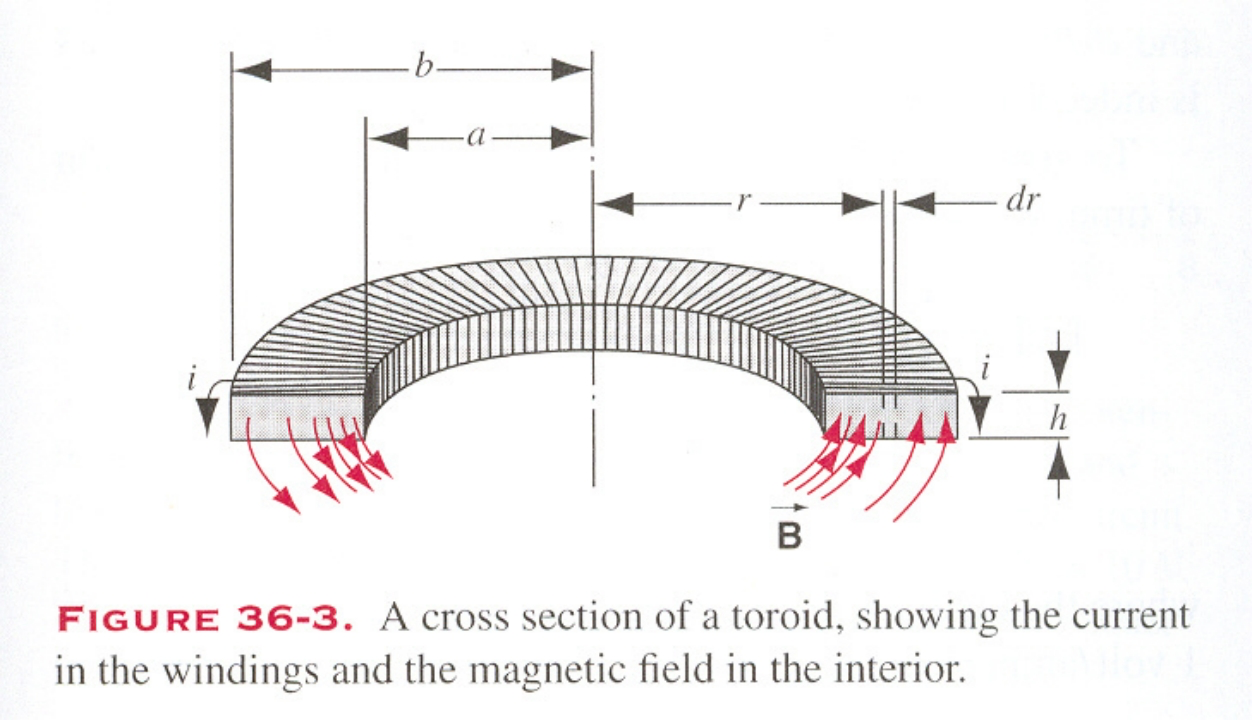
the B of Toroid (N N N
∮ B ⃗ ∙ d l ⃗ = B 2 π r = μ 0 N i → B = μ 0 n i ( n = N 2 π r ) \oint \vec B\bullet \mathrm d \vec l=B2\pi r=\mu_0Ni\to B=\mu _0ni(n=\frac{N}{2\pi r}) ∮ B ∙ d l = B 2 π r = μ 0 N i → B = μ 0 ni ( n = 2 π r N ) ::: tip[Application]
Power door locks
Magnetic cranes
Electronic Switch “relay
:::
32-4 The magnetic force on a carrying-current wire# remember
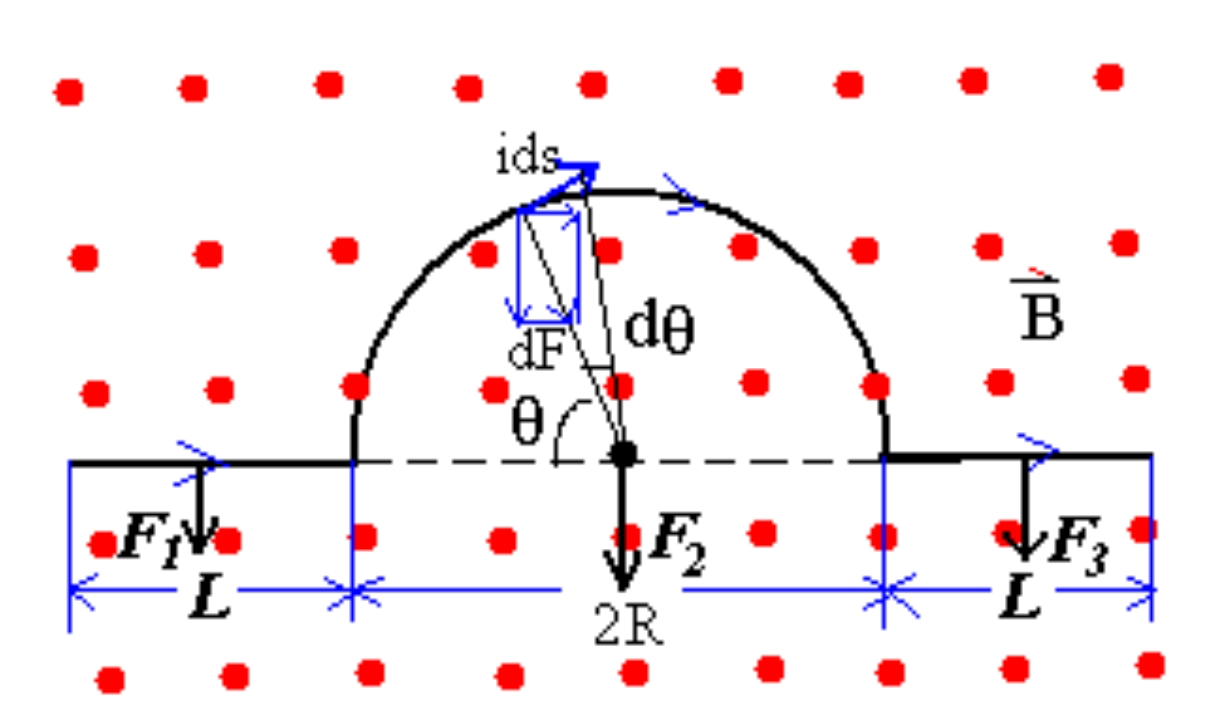
d F ⃗ = i d s ⃗ × B ⃗ ( d F ⃗ 2 = i 2 d s ⃗ 2 × ( ∮ L 1 i 1 d s ⃗ 1 × r ^ 12 r 12 2 ) ) \mathrm d \vec F=i\mathrm d\vec s\times \vec B(\mathrm d \vec F_{2} =i_2\mathrm d\vec s_2\times \left(\oint _{L_1}\frac{i_1\mathrm d \vec s_1 \times \hat r_{12}}{r^2_{12}}\right)) d F = i d s × B ( d F 2 = i 2 d s 2 × ( ∮ L 1 r 12 2 i 1 d s 1 × r ^ 12 ) ) EG32-5,P738
F 2 = F ⊥ = ∫ 0 π i B R d θ sin θ = 2 i B R F_{2}=F_{\perp}=\int_{0}^{\pi}iBR\mathrm d \theta \sin\theta=2iBR F 2 = F ⊥ = ∫ 0 π i BR d θ sin θ = 2 i BR F = F 1 + F 2 + F 3 = i B ( 2 L + 2 R ) F=F_1+F_2+F_3=iB(2L+2R) F = F 1 + F 2 + F 3 = i B ( 2 L + 2 R ) for two parallel conductors
f = μ 0 i 1 i 2 2 π d ⇒ i 1 = i 2 = i i f d μ 0 2 π f=\frac{\mu_0i_1i_2}{2\pi d}\xRightarrow{i_1=i_2=i}i\sqrt{\frac{fd}{\frac{\mu_0}{2\pi}}} f = 2 π d μ 0 i 1 i 2 i 1 = i 2 = i i 2 π μ 0 fd we define i = 1 A i=1A i = 1 A 1 m 1m 1 m 2 × 1 0 − 7 N / m 2\times 10^{-7}N/m 2 × 1 0 − 7 N / m
for convenience sake, we define n ^ \hat n n ^
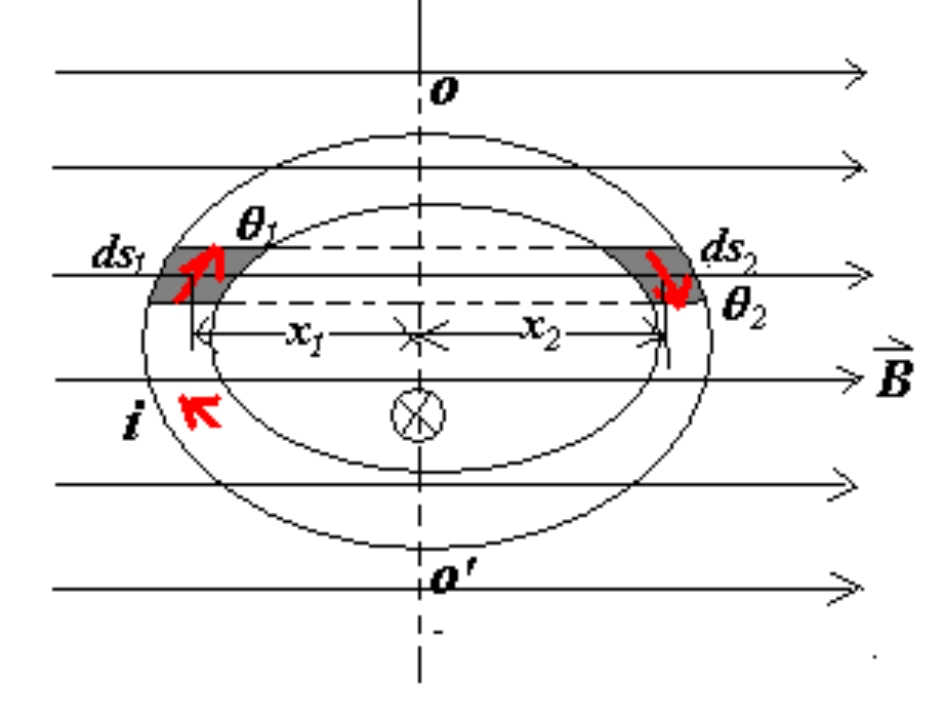
μ ⃗ = i A n ^ τ ⃗ = μ ⃗ × B ⃗ \vec \mu =iA\hat n\\\vec \tau=\vec \mu\times \vec B μ = i A n ^ τ = μ × B this holds for arbitrary shape loop
d F 1 = i d s 1 B sin θ 1 d F 2 = i d s 2 B sin θ 2 d F 1 = d F 2 = i B d h d τ = d F 1 x 1 + d F 2 x 2 = i B d A \begin{aligned}&dF_{1}=ids_{1}B\sin \theta _1\\&dF_2=ids_2 B\sin \theta _2\\&dF_1=dF_2=iBdh\\&d\tau =dF_1x_1+dF_2x_2=iBdA\end{aligned} d F 1 = i d s 1 B sin θ 1 d F 2 = i d s 2 B sin θ 2 d F 1 = d F 2 = i B d h d τ = d F 1 x 1 + d F 2 x 2 = i B d A for magnetic dipole
we define τ ⃗ = i A ( n ⃗ × B ⃗ ) \vec \tau=iA(\vec n \times \vec B) τ = i A ( n × B )
then
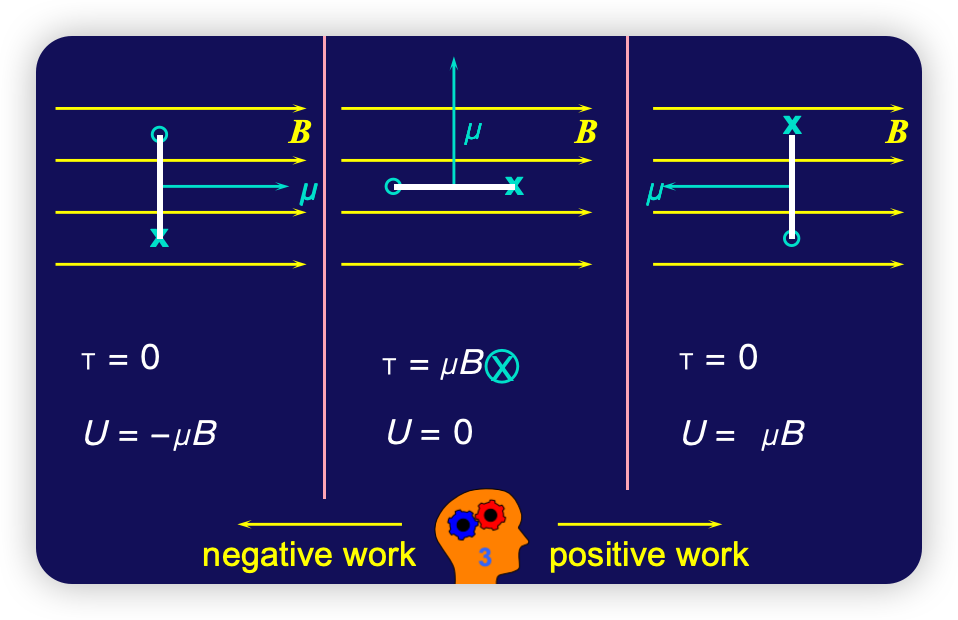
U p = − ∫ ∞ p τ ⋅ d θ ⃗ = ∫ μ B sin θ d θ = μ B cos θ = μ ⃗ ∙ B ⃗ ⇒ U = − μ ∙ B ⃗ U_p=-\int_{\infty}^{p} \tau \cdot d\vec \theta =\int \mu B \sin \theta d\theta=\mu B \cos \theta =\vec \mu \bullet \vec B\Rightarrow U=-\mu \bullet \vec B U p = − ∫ ∞ p τ ⋅ d θ = ∫ μ B sin θ d θ = μ B cos θ = μ ∙ B ⇒ U = − μ ∙ B remind that
p ⃗ = q d ⃗ \vec p=q\vec d p = q d τ ⃗ = p ⃗ × E ⃗ \vec \tau =\vec p\times \vec E τ = p × E U = − p ⃗ ∙ E ⃗ U=-\vec p\bullet \vec E U = − p ∙ E we have
μ = A i ⃗ \mu =A\vec i μ = A i τ ⃗ = μ ⃗ × B ⃗ \vec \tau =\vec \mu \times \vec B τ = μ × B U = − μ ⃗ ∙ B ⃗ U=-\vec \mu \bullet \vec B U = − μ ∙ B
System μ(J/T) Nucleus of N atom 2.0x10^-28 Proton 1.4x10^-26 Electron 9.3x10^-24 N atom 2.8x10^-23 Typical small coil 5.4x10^-6 Small bar magnet 5.0 Superconducting coil 400 The Earth 8.0x10^22
MRI (Magnetic Resonance Imaging)
Proton Spin and Magnetic Moment:
A single proton possesses a positive charge + ∣ e ∣ +|e| + ∣ e ∣ Naively imagining the charge circulating in a loop gives rise to a magnetic dipole moment μ \mu μ Behavior in an External Magnetic Field ( B ):
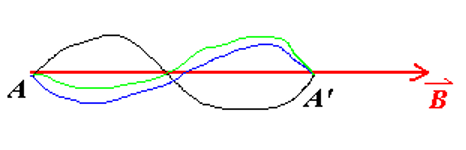
Classically: Torques will be present unless the magnetic moment μ ⃗ \vec{\mu} μ
Quantum Mechanics (QM): The spin is always aligned either with or against the magnetic field ( B ).
Anti-aligned State: Energy U 2 = μ B U_2 = \mu B U 2 = μ B Aligned State: Energy U 1 = − μ B U_1 = -\mu B U 1 = − μ B Energy Difference: Δ U = U 2 − U 1 = 2 μ B \Delta U = U_2 - U_1 = 2\mu B Δ U = U 2 − U 1 = 2 μ B
μ p r o t o n = 1.36 × 1 0 − 26 A m 2 B = 1 Tesla ( = 1 0 4 G a u s s ) Δ U = 2 μ B = 2.7 × 1 0 − 26 J \begin{aligned}&\mu_{proton}=1.36\times10^{-26}\mathrm{~A~m}^2\quad B=1\text{ Tesla }(=10^4\mathrm{~Gauss})\\&\Delta U=2\mu B=2.7\times10^{-26}\mathrm{J}\end{aligned} μ p ro t o n = 1.36 × 1 0 − 26 A m 2 B = 1 Tesla ( = 1 0 4 Gauss ) Δ U = 2 μ B = 2.7 × 1 0 − 26 J h ν = Δ U ⇒ ν = 2.7 × 1 0 − 26 6.6 × 1 0 − 34 J s = 41 M H z h\nu =\Delta U\Rightarrow \nu=\frac{2.7\times 10^{-26}}{6.6\times 10^{-34}Js}=41\mathrm{MHz} h ν = Δ U ⇒ ν = 6.6 × 1 0 − 34 J s 2.7 × 1 0 − 26 = 41 MHz
more applications
app
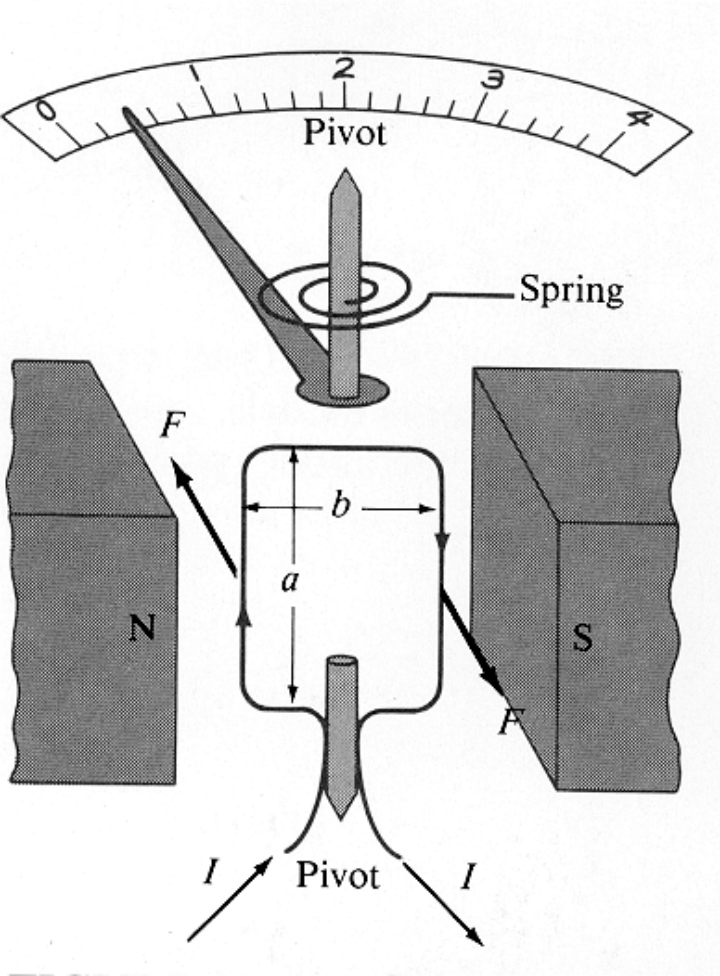
Magnetic Force on a Current Loop: When a loop of wire carrying an electric current is placed in a magnetic field, the field exerts a torque on the loop, attempting to align the loop’s magnetic dipole moment with the field. Structure of a Galvanometer: Inside a galvanometer, there is a rotating coil attached to a pivot. To return the pointer to its equilibrium position, a spring is included in the galvanometer, which creates a torque in the opposite direction to the rotation of the coil. motor is almost the same ,we just skip it
fixed voltage fixed current 32-5 The motion of a charge in a magnetic field# we define Lorentz Force as
F ⃗ = q v ⃗ × B ⃗ F = q v B sin θ \begin{align*} \vec F &=q\vec v\times \vec B\\ F&=qvB\sin \theta \end{align*} F F = q v × B = q v B sin θ we can find that
F ⃗ L = q v ⃗ × B ⃗ \vec F_L=q\vec v \times \vec B F L = q v × B
d F ⃗ A = i d s ⃗ × B ⃗ \mathrm d \vec F_A = id \vec s \times \vec B d F A = i d s × B
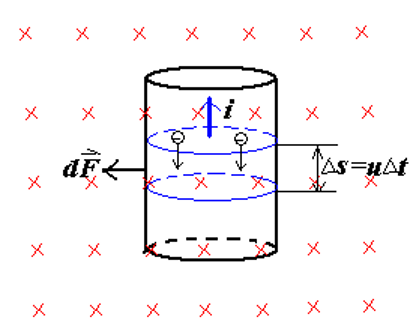
from this image we can confirm that
Δ q = e n A u Δ t i = Δ q Δ t = n A u e u ⃗ ⊥ B ⃗ , sin θ = 1 , f L = e u B F A = n A × Δ s f L = B i Δ s \begin{align*} \Delta q=enAu\Delta t\\ i=\frac{\Delta q}{\Delta t}=nAue\\ \vec u\perp \vec B,\sin \theta =1,f_L=euB\\ F_A=nA\times \Delta s f_L=Bi\Delta s \end{align*} Δ q = e n A u Δ t i = Δ t Δ q = n A u e u ⊥ B , sin θ = 1 , f L = e u B F A = n A × Δ s f L = B i Δ s then let’s talk about the motion of a charged part. in a magnetic field
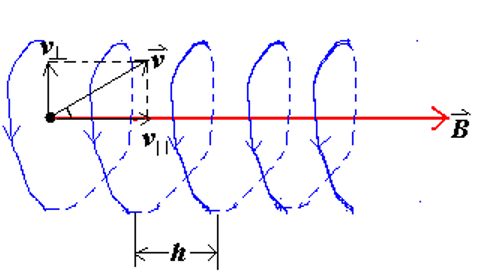
v ⃗ ⊥ B ⃗ \vec v\perp \vec B v ⊥ B
v ⊥ = v sin θ , v ∣ ∣ = v cos θ v_\perp =v\sin \theta ,v_{||} =v\cos \theta v ⊥ = v sin θ , v ∣∣ = v cos θ
Period : T = 2 π R v ⊥ T=\frac{2\pi R}{v\perp} T = v ⊥ 2 π R h = v ∣ ∣ T = 2 π m v ∣ ∣ q B h=v_{||}T =\frac{2\pi mv_{||}}{qB} h = v ∣∣ T = qB 2 πm v ∣∣ app
R = m v ⊥ q B h = 2 π m v q B θ → 0 , v ⊥ → v θ , v ∣ ∣ → v R=\frac{mv_\perp}{qB}\\ h=\frac{2\pi mv }{qB}\\ \theta \to 0,v_\perp \to v\theta ,v_{||}\to v R = qB m v ⊥ h = qB 2 πm v θ → 0 , v ⊥ → v θ , v ∣∣ → v in uniform magnetic field
the path is just circles(directions following the signal of charge)
the detailed application is
convex lens magnetic mirror app
R = m v p e r p q B R=\frac{mv_perp}{qB} R = qB m v p er p the magnetic bottle is to confine the hot ionized gases and control the thermonuclear fusion
when taking the strong B, and we can have a small R constraint
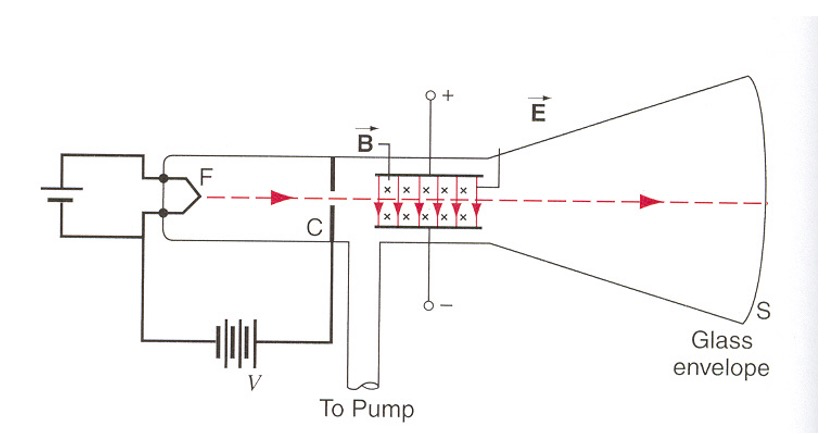
discovery of electron by J.J.Thomson in 1897
F ⃗ = q E ⃗ + q v ⃗ × B ⃗ e E = e v B ⇒ v = E B y = 1 2 e E m ( L v ) 2 = e E L 2 2 m v 2 ⇒ e m = 2 y E B 2 L 2 = 1.759 × 1 0 11 C / k g \begin{align*} \vec F=q\vec E+q\vec v\times \vec B\\eE=evB\Rightarrow v=\frac{E}{B}\\y=\frac{1}{2}\frac{eE}{m}\left(\frac{L}{v}\right)^2=\frac{eEL^2}{2mv^2}\\\Rightarrow\frac{e}{m}=\frac{2yE}{B^2L^2} =1.759\times 10^{11}C/kg \end{align*} F = q E + q v × B e E = e v B ⇒ v = B E y = 2 1 m e E ( v L ) 2 = 2 m v 2 e E L 2 ⇒ m e = B 2 L 2 2 y E = 1.759 × 1 0 11 C / k g mass spectrometer
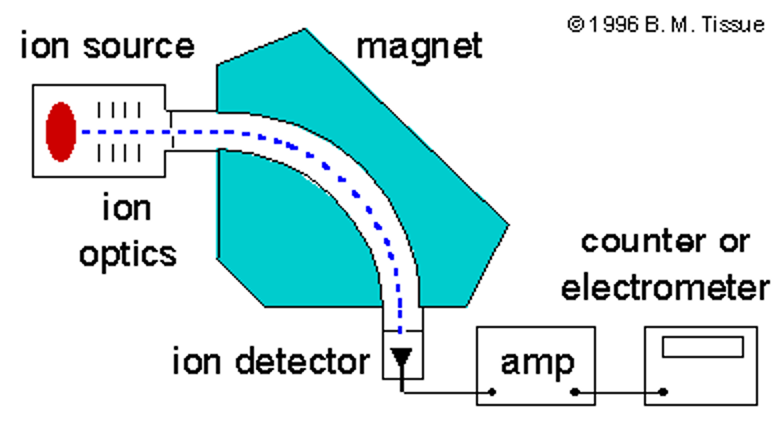
R = m v q B 1 2 m v 2 = q V ⇒ m q = R 2 B 2 2 V R=\frac{mv}{qB}\\\frac{1}{2}mv^2=qV \\\Rightarrow \frac{m}{q}=\frac{R^2B^2}{2V} R = qB m v 2 1 m v 2 = q V ⇒ q m = 2 V R 2 B 2 detailedly we accelerate electrons in a known potential U = q v U=qv U = q v
with looking at the m / q m/q m / q
paleoceanography space exploration detect chemical and bio. Weapons(anthrax ) movement measurement
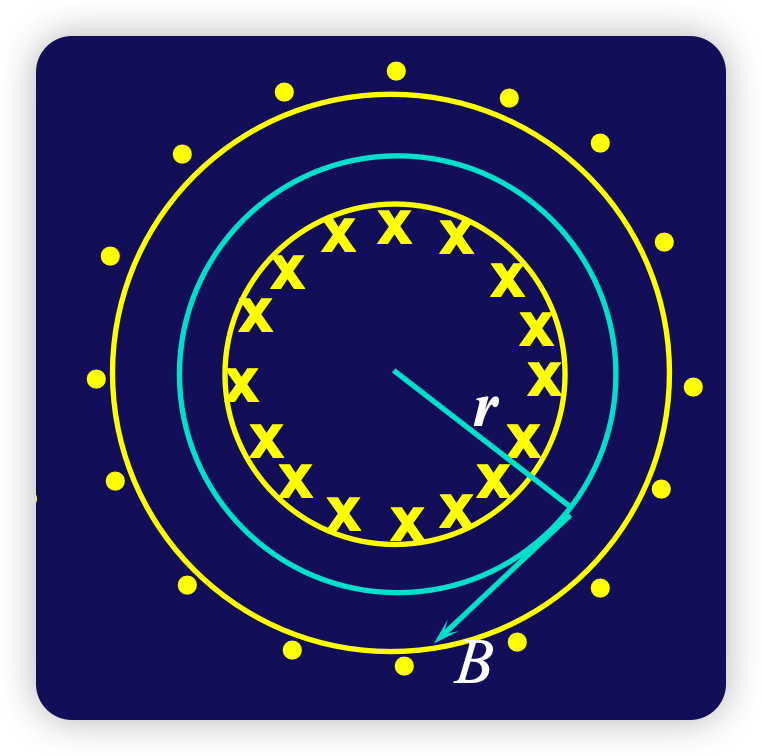
R = m v q B = 2 m K q B R=\frac{mv}{qB}=\frac{\sqrt {2mK}}{qB} R = qB m v = qB 2 m K the cyclotron
q v B = m v 2 R f = q B 2 π m v M = B R q m E K = 1 2 m v M 2 = B 2 R 2 q 2 2 m qvB=m\frac{v^2}{R}\\ f=\frac{qB}{2\pi m}\\ v_M=BR\frac{q}{m}\\ E_K=\frac{1}{2}mv_M^2 =\frac{B^2R^2q^2}{2m} q v B = m R v 2 f = 2 πm qB v M = BR m q E K = 2 1 m v M 2 = 2 m B 2 R 2 q 2
with relaticity effect
m = m 0 1 − v 2 c 2 T = 2 π m 0 q B × 1 1 − v 2 c 2 B 1 − v 2 c 2 = c o n s t \begin{align} m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\\ T=\frac{2\pi m_0}{qB}\times \frac{1}{\sqrt {1-\frac{v^2}{c^2}}}\\ B\sqrt{1-\frac{v^2}{c^2}}=\mathrm {const} \end{align} m = 1 − c 2 v 2 m 0 T = qB 2 π m 0 × 1 − c 2 v 2 1 B 1 − c 2 v 2 = const for proton
v c = 0.3 → 1 − v 2 c 2 = 0.95 \frac{v}{c}=0.3 \rightarrow \sqrt{1-\frac{v^2}{c^2}}=0.95 c v = 0.3 → 1 − c 2 v 2 = 0.95 we can have synchrotron withe much larger magnitude B and N
The Hall Effect#
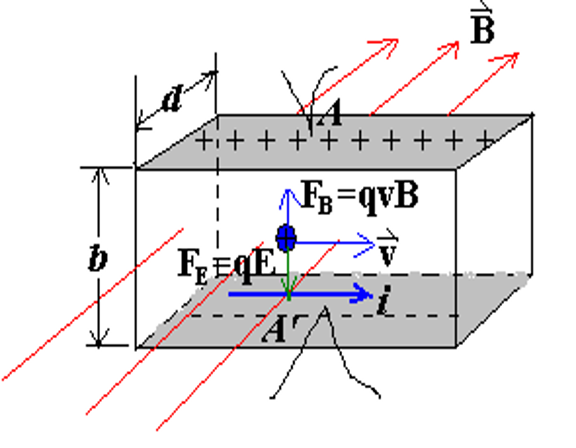
when at equilibrium
q v B = q E , E = v B V A A ′ = v B b = j n q B b = i B n q d = κ i B d \begin{align} qvB=qE,E=vB\\ V_{AA'}=vBb=\frac{j}{nq} Bb=\frac{iB}{nqd}=\kappa \frac{iB}{d}\\ \end{align} q v B = qE , E = v B V A A ′ = v B b = n q j B b = n q d i B = κ d i B (remember j ⋅ b ⋅ d ≡ i j\cdot b\cdot d\equiv i j ⋅ b ⋅ d ≡ i
we define the charge drift speed as v v v n n n R H R_H R H
n = i B q d 1 V A A ′ R H = V A A ′ i = B n q d n=\frac{iB}{qd}\frac{1}{V_{AA'}}\\R_H=\frac{V_{AA'}}{i}=\frac{B}{nqd} n = q d i B V A A ′ 1 R H = i V A A ′ = n q d B the quantized hall effect
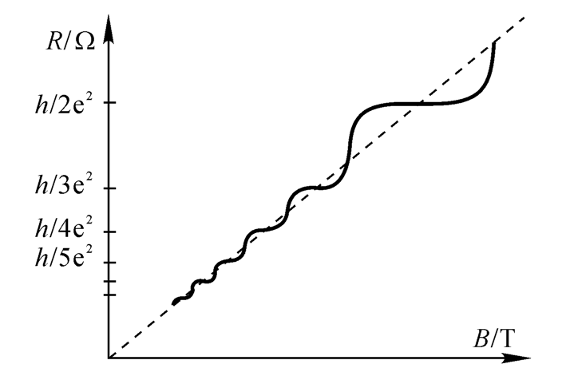
when detect hall effect on two-dimensional hall effect , it;s displayed not linearly
Δ H i = B n q d \frac{\Delta _H}{i}=\frac{B}{nqd} i Δ H = n q d B
with const n , q , d n,q,d n , q , d R H ∝ B R_H\propto B R H ∝ B
1986 Nobel Prize h e 2 = 25812.806 Ω \frac{h}{e^2}=25812.806\Omega e 2 h = 25812.806Ω
App of Hall effect# Measure B Measure i P Transfer DC->AC a specific field is ABS: work as B tensor,detect shaft rotation speed and beam oscillating voltage
V A A ′ = 1 n q ⋅ i B d V_{AA'} = \frac{1}{nq}\cdot \frac{iB}{d} V A A ′ = n q 1 ⋅ d i B Chap 34 The Faraday’s Law of Induction# General Review# Electrostaticsmotion of q q q E ⃗ \vec E E ∫ E ⃗ ⋅ d A ⃗ = ∑ q c l s ε \displaystyle \int \vec E\cdot d\vec A =\frac{\sum q_{cls}}{\varepsilon} ∫ E ⋅ d A = ε ∑ q c l s Magnetostaticsmotion of q q q B ⃗ \vec B B Electrodynamicsd B ⃗ d t ≠ 0 ⇒ E ⃗ \frac{d\vec B}{d t}\neq 0\Rightarrow \vec E d t d B = 0 ⇒ E AC circuit,inductors,transformers d E ⃗ d t ≠ 0 ⇒ B ⃗ \frac{d\vec E}{d t}\neq 0\Rightarrow \vec B d t d E = 0 ⇒ B 34-1/2 Basic Phenomena & Faraday’s Law of Induction# d Φ B d t → i i n d ε = − d Φ B d t \frac{d\Phi_B}{dt}\to i_{ind}\\ \varepsilon =-\frac{d\Phi_B}{dt} d t d Φ B → i in d ε = − d t d Φ B just treat ε \varepsilon ε
34-3 Lenz’s Law# The induced current will appear in such a direction that it opposes the change in flux that produced it.
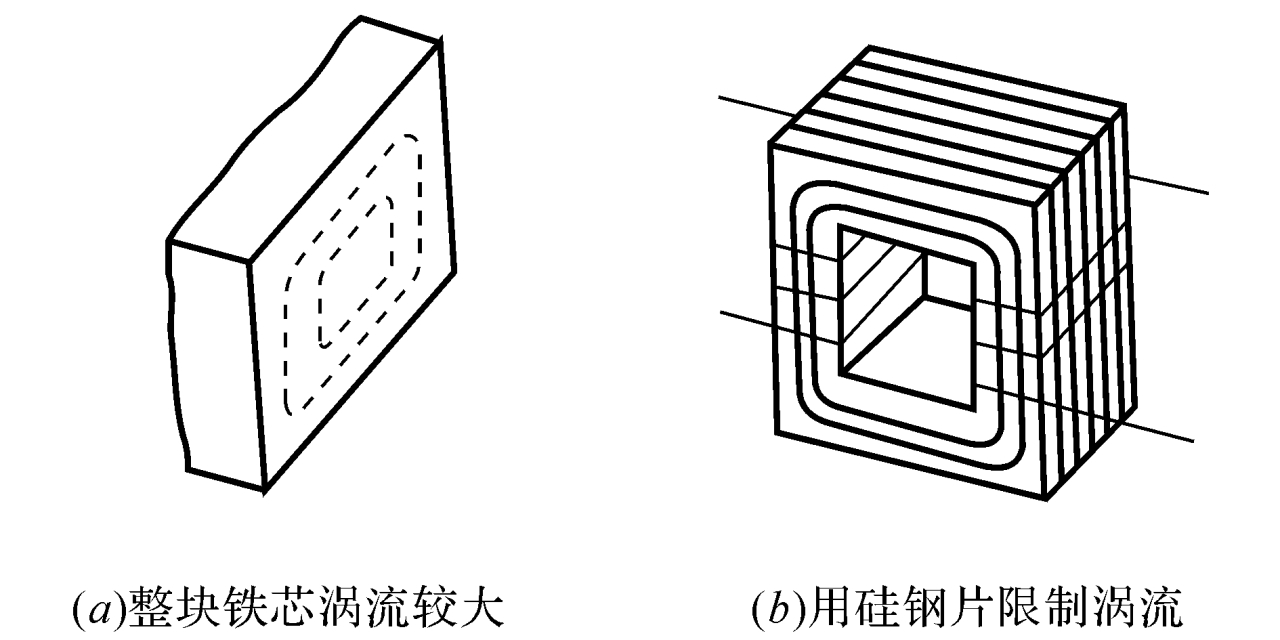
laminated materials can reduce eddy currents
app : magnetic Induction
E-M Cannon: alternating voltage to a solenoid ,then the flux changes -> current -> force Tape/Hard Drive/ZIP Readout : Tiny coil responds to change in flux as the magnetic domains (encoding 0’s or 1’s) go by.Credit Card Reader Magnetic Levitation (Maglev) Trains : eddy currents produce field in opposite direction34-4 Motional emf and Induced emf# Motional emf: d S d t → d Φ d t → ε \frac{d S}{d t}\to \frac{d\Phi}{dt}\to \varepsilon d t d S → d t d Φ → ε Induced emf: d B d t → d Φ d t → ε \frac{d B}{d t}\to \frac{d\Phi}{dt}\to \varepsilon d t d B → d t d Φ → ε Motional emf# Lorentz force results in a motional emf
f ⃗ = − e ( v ⃗ × B ⃗ ) \vec f =-e(\vec v\times \vec B) f = − e ( v × B ) Non electrostatic force
K ⃗ = f ⃗ − e = v ⃗ × B ⃗ \vec K=\frac{\vec f}{-e}=\vec v\times \vec B K = − e f = v × B Motional emf
ε = ∫ − + K ⃗ ∙ d l ⃗ = ∫ C D ( v ⃗ × B ⃗ ) ⋅ d l ⃗ \varepsilon =\int_{-}^+ \vec K \bullet d\vec l=\int_{C}^D (\vec v\times \vec B)\cdot d\vec l ε = ∫ − + K ∙ d l = ∫ C D ( v × B ) ⋅ d l Lorentz force can’t do work to electron
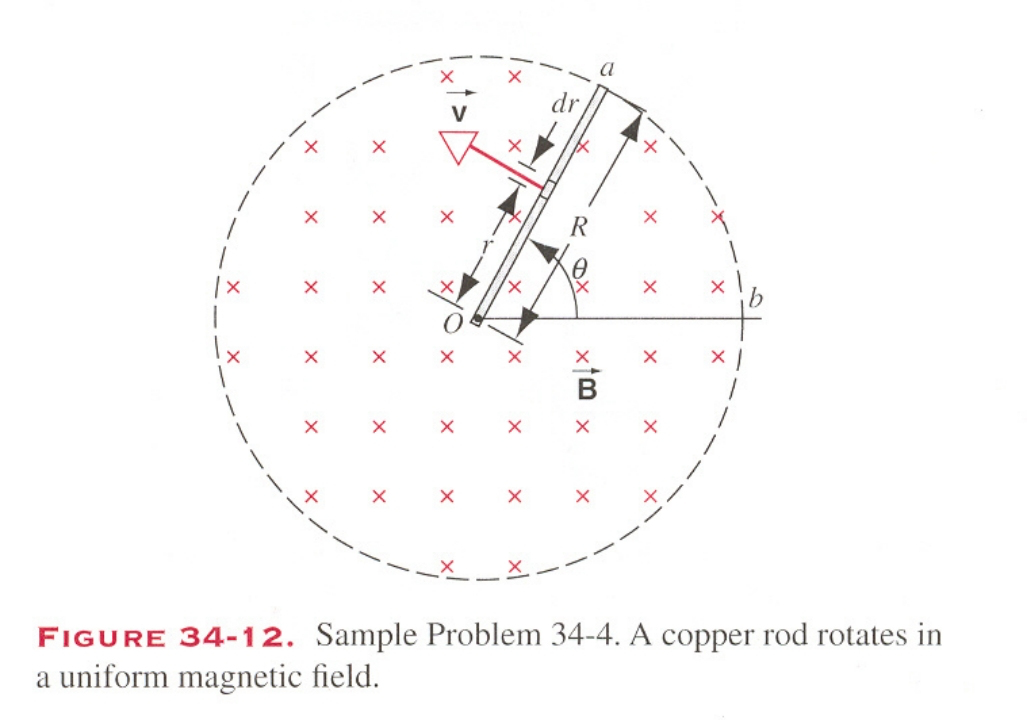
P781 34-4
Sol1:
d ε = ( v ⃗ × B ⃗ ) ⋅ d r ⃗ = − B v d r ε = − 1 2 B ω R 2 d\varepsilon =(\vec v\times \vec B)\cdot d\vec r =-Bvdr\\ \varepsilon =-\frac{1}{2}B\omega R^2 d ε = ( v × B ) ⋅ d r = − B v d r ε = − 2 1 B ω R 2 Sol2:
ε = − d Φ B d t = − 1 2 d B ( 1 2 R 2 θ ) d t \varepsilon =\frac{-d\Phi_B}{dt}=-\frac{1}{2}\frac{dB(\frac{1}{2}R^2\theta)}{dt} ε = d t − d Φ B = − 2 1 d t d B ( 2 1 R 2 θ ) direction +o -a
App
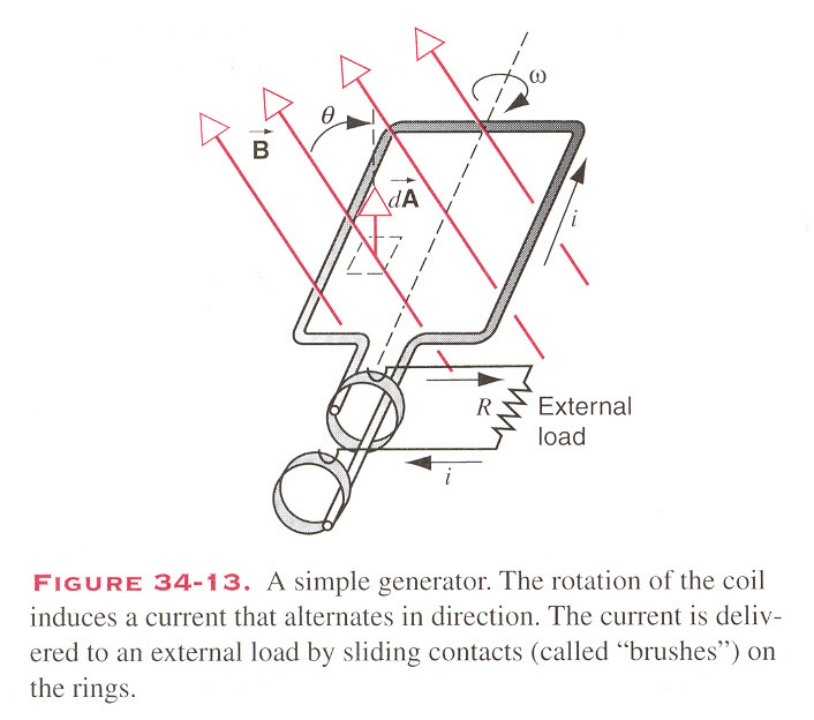
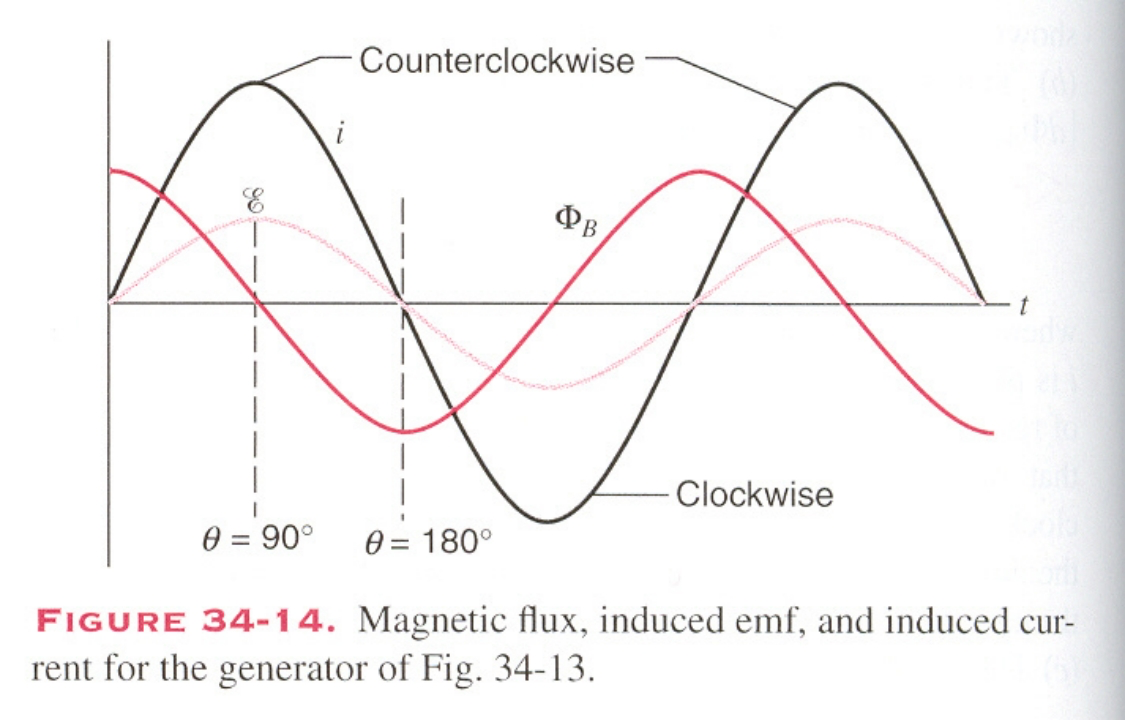
Φ B = B A cos ω t ε = B A ω sin ω t \Phi_B=BA\cos \omega t\\\varepsilon =BA\omega \sin \omega t Φ B = B A cos ω t ε = B A ω sin ω t Induced emf# a increasing magnetic field pass through the loop will generate a ringing electric field.
ε = ∮ E ⃗ ⋅ d l ⃗ \varepsilon =\oint \vec E\cdot d\vec l ε = ∮ E ⋅ d l
ε = − d Φ B d t = − A k \varepsilon =-\frac{d\Phi_B}{dt}=-Ak ε = − d t d Φ B = − A k W = ε q 0 = q 0 E i n d u c e d ⋅ 2 π r ε = E i n d u c e d ⋅ 2 π r = ∮ E ⃗ i n d u c e d ⋅ d l ⃗ \begin{aligned}&W=\varepsilon q_{0}=q_{0}E_{induced}\cdot2\pi r\\&\varepsilon=E_{induced}\cdot2\pi r=\oint\vec{E}_{induced}\cdot d\vec{l}\end{aligned} W = ε q 0 = q 0 E in d u ce d ⋅ 2 π r ε = E in d u ce d ⋅ 2 π r = ∮ E in d u ce d ⋅ d l ε = − d Φ B d t ∴ ∮ E ⃗ i n d u c e d ⋅ d l ⃗ = − d Φ B d t \varepsilon=-\frac{d\Phi_{B}}{dt}\\\therefore\quad\oint\vec{E}_{induced}\cdot d\vec{l}=-\frac{d\Phi_{B}}{dt} ε = − d t d Φ B ∴ ∮ E in d u ce d ⋅ d l = − d t d Φ B it just implide that
∇ × E ⃗ = − ∂ B ⃗ ∂ t \nabla \times \vec E=-\frac{\partial \vec B}{\partial t} ∇ × E = − ∂ t ∂ B E ⃗ = E ⃗ s t a + E ⃗ i n d ∴ ∮ E ⃗ ⋅ d l ⃗ = ∮ ( E ⃗ s t a + E ⃗ i n d ) ⋅ d l ⃗ = 0 + ( − d Φ B d t ) = − d Φ B d t \begin{aligned}&\vec{E}=\vec{E}_{sta}+\vec{E}_{ind}\\&\therefore\quad\oint\vec{E}\cdot d\vec{l}=\oint(\vec{E}_{sta}+\vec{E}_{ind})\cdot d\vec{l}=0+(-\frac{d\Phi_B}{dt})=-\frac{d\Phi_B}{dt}\end{aligned} E = E s t a + E in d ∴ ∮ E ⋅ d l = ∮ ( E s t a + E in d ) ⋅ d l = 0 + ( − d t d Φ B ) = − d t d Φ B Es is set up by charges, Ein is set up by changing magnetic field. Both kinds of electric field exert on charges.
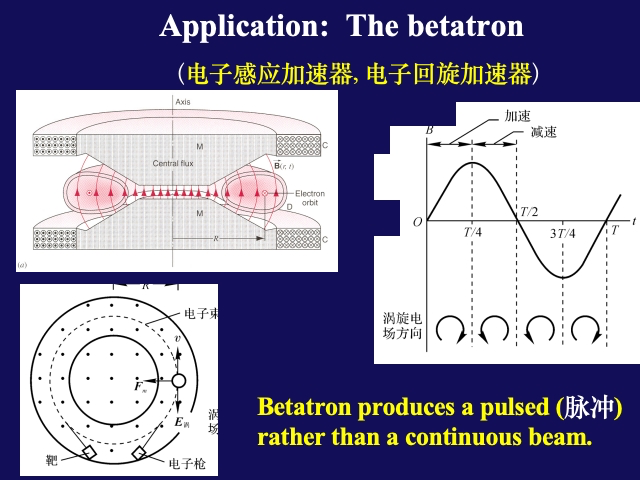
The betatron
Betatron produces a pulse rather than a continuous beam.
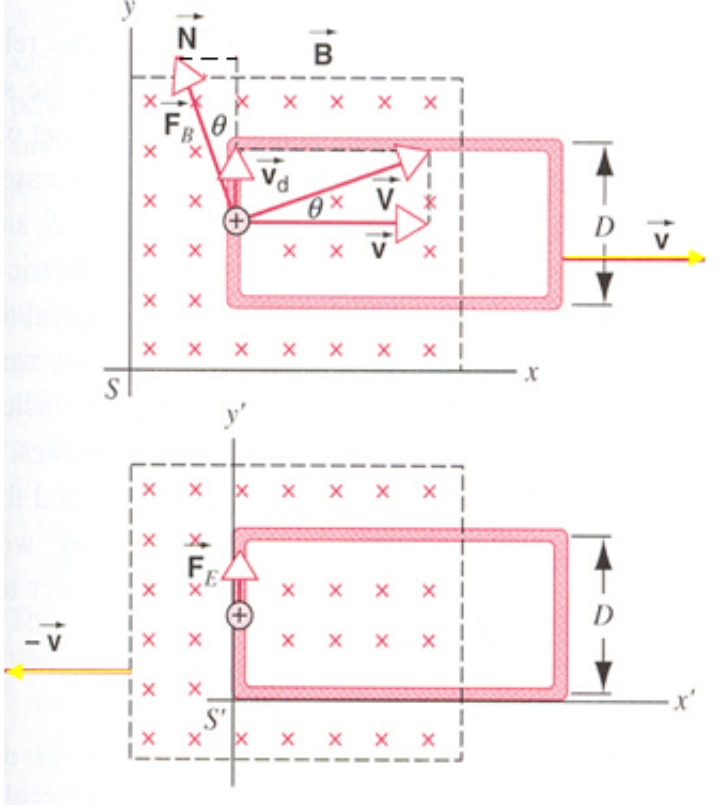
34-5. Induction & Relative Motion#
Motional emf: V ⃗ = ν ⃗ + ν ⃗ a , F ⃗ b = N ⃗ + F ⃗ i d W N = N ( ν d t ) = F B sin θ ( ν d t ) = ( q V B ) ( ν d / V ) ( ν d t ) = ( q B ν d ) ( ν d t ) = ( q B ν ) ( ν d d t ) = q B ν d l W N = ∫ q B v d l = q B v D ε = W N / q = B D v d W i = − F i d l = − q v B d l W i = − q v B D = − W N \begin{aligned}&\text{Motional emf:}\\&\vec{V}=\vec{\nu}+\vec{\nu}_{a},\quad\vec{F}_{b}=\vec{N}+\vec{F}_{i}\\&\mathrm{d}W_{N}=N(\nu\mathrm{d}t)\\&=F_{B}\sin\theta(\nu\mathrm{d}t)\\&=(qVB)(\nu_{d}/V)(\nu\mathrm{d}t)\\&=(qB\nu_{d})(\nu\mathrm{d}t)\\&=(qB\nu)(\nu_{d}\mathrm{d}t)\\&=qB\nu dl\\&W_N=\int qBvdl=qBvD\\&\varepsilon = W_N/q=BDv \\&dW_i=-F_idl=-qvBdl\\&W_i=-qvBD=-W_N\end{aligned} Motional emf: V = ν + ν a , F b = N + F i d W N = N ( ν d t ) = F B sin θ ( ν d t ) = ( q V B ) ( ν d / V ) ( ν d t ) = ( qB ν d ) ( ν d t ) = ( qB ν ) ( ν d d t ) = qB ν d l W N = ∫ qB v d l = qB v D ε = W N / q = B D v d W i = − F i d l = − q v B d l W i = − q v B D = − W N ε = ∫ ( E ⃗ ′ + v ⃗ × B ⃗ ) ⋅ d l ⃗ \varepsilon =\int (\vec E'+\vec v\times \vec B)\cdot d\vec l ε = ∫ ( E ′ + v × B ) ⋅ d l
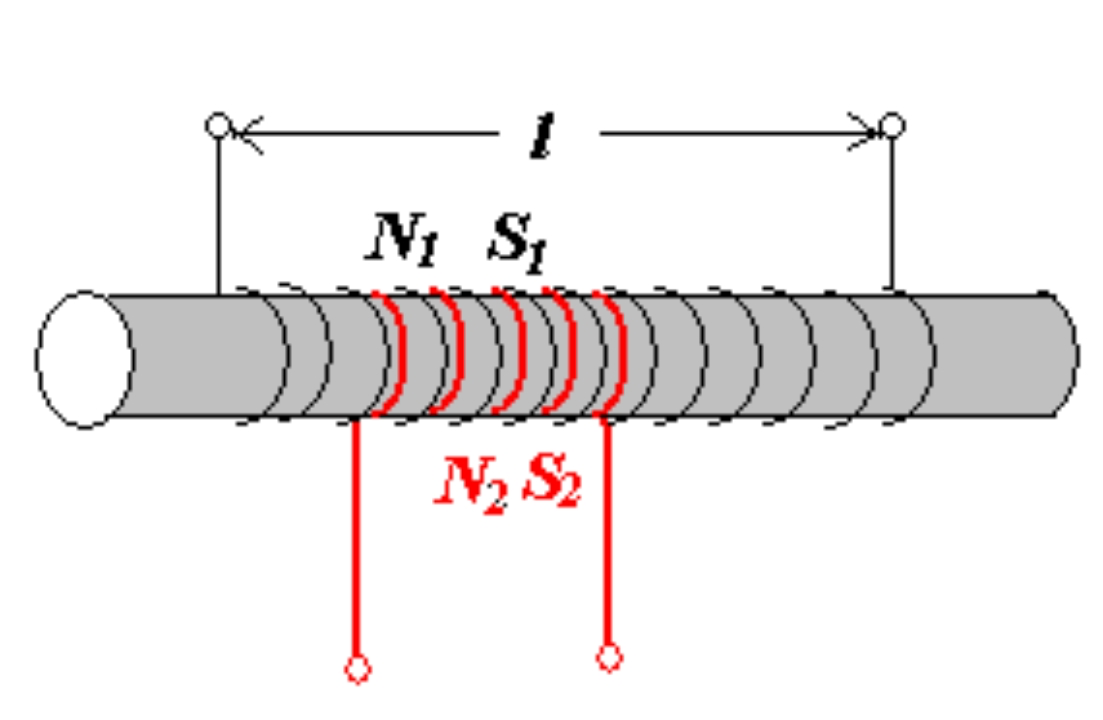
Chapter 35(36) Inductance and Magnetic properties of materials# 35-1 Inductance# Mutual Inductance# i1 change s2 induced emf ε 2 \varepsilon _2 ε 2
i2 change s1 induced emf ε 1 \varepsilon _1 ε 1
M 12 = Ψ 12 i 1 = N 2 Φ 12 i 1 ; ε 2 = − d Ψ 12 d t = − M 12 d i 1 d t , ( i 1 c h a n g e ) M 21 = Ψ 21 i 2 = N 1 Φ 21 i 2 ; ε 1 = − d Ψ 21 d t = − M 21 d i 2 d t , ( i 2 c h a n g e ) M_{12}=\frac{\Psi_{12}}{i_{1}}=\frac{N_{2}\Phi_{12}}{i_{1}};\quad\varepsilon_{2}=-\frac{d\Psi_{12}}{dt}=-M_{12} \frac{di_{1}}{dt},\quad(i_{1} \mathrm{change})\\M_{21}=\frac{\Psi_{21}}{i_{2}}=\frac{N_{1}\Phi_{21}}{i_{2}};\quad\varepsilon_{1}=-\frac{d\Psi_{21}}{dt}=-M_{21} \frac{di_{2}}{dt},\quad(i_{2} \mathrm{change}) M 12 = i 1 Ψ 12 = i 1 N 2 Φ 12 ; ε 2 = − d t d Ψ 12 = − M 12 d t d i 1 , ( i 1 change ) M 21 = i 2 Ψ 21 = i 2 N 1 Φ 21 ; ε 1 = − d t d Ψ 21 = − M 21 d t d i 2 , ( i 2 change ) M 12 , M 21 M_{12},M_{21} M 12 , M 21
B = μ 0 n i , B 1 = μ 0 N 1 l i 1 Ψ 12 = N 2 B 1 A = μ 0 N 1 N 2 A l i 1 ε 2 = − M d i 1 d t M 12 = Ψ 12 i 1 = μ 0 N 1 N 2 A l = − 25 × 1 0 − 6 × 10 V = 4 π ⋅ 1 0 − 7 1000 × 20 × 1 0 − 3 1 ∣ = − 250 μ V = 25 × 1 0 − 6 H = 25 μ H \begin{aligned} &B=\mu_{0}ni, B_{1}=\mu_{0} \frac{N_{1}}{l}i_{1} \\ &\Psi_{_{12}}=N_{_2}B_{_1}A=\mu_{_0} \frac{N_{_1}N_{_2}A}{l}i_{_1}&& \varepsilon_{2}=-M\frac{di_{1}}{dt} \\ &M_{12}=\frac{\Psi_{_{12}}}{i_{_1}}=\mu_{_0}\frac{N_{_1}N_{_2}A}{l}&& =-25\times10^{-6}\times10V \\ &=4\pi\cdot10^{-7}\frac{1000\times20\times10^{-3}}{1}&& |=-250 \mu V \\ &=25\times10^{-6}H=25 \mu H \\ \end{aligned} B = μ 0 ni , B 1 = μ 0 l N 1 i 1 Ψ 12 = N 2 B 1 A = μ 0 l N 1 N 2 A i 1 M 12 = i 1 Ψ 12 = μ 0 l N 1 N 2 A = 4 π ⋅ 1 0 − 7 1 1000 × 20 × 1 0 − 3 = 25 × 1 0 − 6 H = 25 μ H ε 2 = − M d t d i 1 = − 25 × 1 0 − 6 × 10 V ∣ = − 250 μ V App
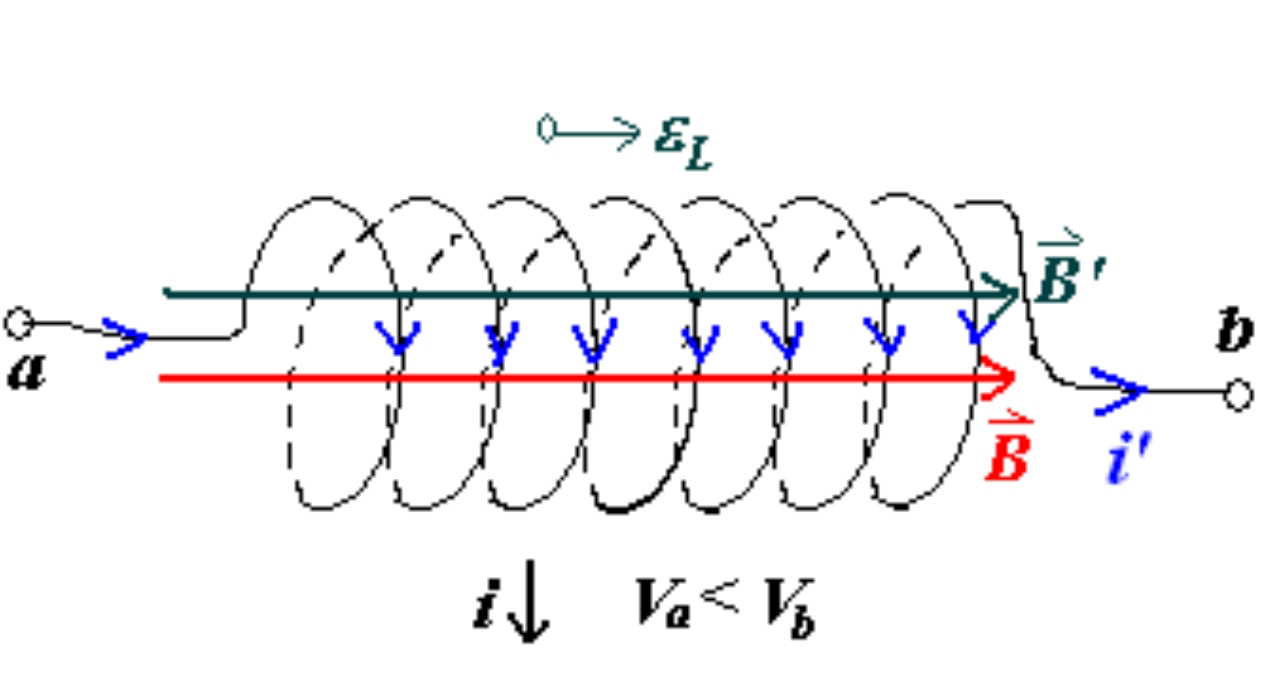
Transformers Airport Metal Detectors Pacemaker Self-Inductance#
ψ = N B A = L i ε L = − d ψ d t = − L d i d t V b − V a = − L d i d t \begin{aligned}&\psi=NBA=Li\\&\varepsilon_{L}=-\frac{d\psi}{dt}=-L\frac{di}{dt}\\&V_{b}-V_{a}=-L\frac{di}{dt}\end{aligned} ψ = NB A = L i ε L = − d t d ψ = − L d t d i V b − V a = − L d t d i L —— self-inductance
L = ∬ B ⃗ ⋅ d A ⃗ i L=\frac{\displaystyle \iint \vec B \cdot d\vec A }{i} L = i ∬ B ⋅ d A ε = − d Φ B d t = − L d i d t \varepsilon =-\frac{d\Phi_B }{dt}=-L\frac{di}{dt} ε = − d t d Φ B = − L d t d i how to calculate self-inductance?
i , B ⃗ , N → L i,\vec B,N\to L i , B , N → L
L = N Φ B i → ε L = − d ( N Φ B ) d t L=\frac{N\Phi_B}{i}\to\varepsilon _L =-\frac{d(N\Phi_B)}{dt} L = i N Φ B → ε L = − d t d ( N Φ B )
Toroid of rectangular
∮ B ⃗ ∙ d l ⃗ = μ 0 N i B = μ 0 i N 2 π r Φ B = ∫ ∫ B ⃗ ∙ d A ⃗ = ∫ a b μ 0 i N 2 π r h d r = μ 0 i N h 2 π ∫ a b d r r = μ 0 i N h 2 π ln b a ∴ L = N Φ B i = μ 0 N 2 h 2 π ln b a \begin{gathered} \oint\vec{B}\bullet d\vec{l}=\mu_0N\boldsymbol{i} \\ B=\frac{\mu_0\boldsymbol{i}N}{2\pi r} \\ \boldsymbol{\Phi}_B=\int\int\vec{B}\bullet d\vec{A}=\int_a^b\frac{\mu_0\boldsymbol{i}N}{2\pi r}\boldsymbol{h}\mathrm{d}r \\ =\frac{\mu_0iNh}{2\pi}\int_a^b\frac{\mathrm{d}r}r=\frac{\mu_0iNh}{2\pi}\ln\frac ba\quad\therefore L=\frac{N\boldsymbol{\Phi}_B}i=\frac{\mu_0N^2\boldsymbol{h}}{2\pi}\ln\frac ba \end{gathered} ∮ B ∙ d l = μ 0 N i B = 2 π r μ 0 i N Φ B = ∫∫ B ∙ d A = ∫ a b 2 π r μ 0 i N h d r = 2 π μ 0 i N h ∫ a b r d r = 2 π μ 0 i N h ln a b ∴ L = i N Φ B = 2 π μ 0 N 2 h ln a b