普物二总结——电学部分# About the tutor
Prof.FangMinghu
[email protected]
Intro# All of simple physics in 5 equations
1. F = q ( E + ν × B ) 2. ∭ E ⋅ d A = Q i n s i d e ε 0 3. ∭ B ⋅ d A = 0 4. ∬ E ⋅ d l = − d Φ B d t 5. ∬ B ⋅ d l = μ 0 I + μ 0 ε 0 d Φ E d t \begin{aligned}&1. F=q(E+\nu\times B)\\&2.\iiint E\cdot dA=\frac{Q_{inside}}{\varepsilon_0}\\&3.\iiint B\cdot dA=0\\&4. \iint E\cdot dl=-\frac{d\Phi_B}{dt}\\&5. \iint B\cdot dl =\mu_0I+\mu_0\varepsilon_0 \frac{d\Phi_E}{dt}\end{aligned} 1. F = q ( E + ν × B ) 2. ∭ E ⋅ d A = ε 0 Q in s i d e 3. ∭ B ⋅ d A = 0 4. ∬ E ⋅ d l = − d t d Φ B 5. ∬ B ⋅ d l = μ 0 I + μ 0 ε 0 d t d Φ E Gravity , Electric and Magnetic Force has magical similarity!
Chap. 25 Charge and Coulomb’s law# Crucial constant nums
e = 1.602 × 1 0 − 19 C e=1.602\times 10^{-19}C e = 1.602 × 1 0 − 19 C
k = 1 4 π ε 0 = 9 × 1 0 9 N ⋅ m 2 ⋅ C − 2 k=\frac{1}{4\pi \varepsilon _0}=9\times 10^{9}N\cdot m^2\cdot C^{-2} k = 4 π ε 0 1 = 9 × 1 0 9 N ⋅ m 2 ⋅ C − 2
1 C = 6 × 1 0 18 e 1C=6\times 10^{18}e 1 C = 6 × 1 0 18 e
m e = 9.1 × 1 0 − 31 k g m_e=9.1\times 10^{-31}kg m e = 9.1 × 1 0 − 31 k g
25-2# 1 n , 1 p = 3 q u a r k s 1n,1p=3 \mathrm{~quarks} 1 n , 1 p = 3 quarks
1 p ( + e ) = 2 × ( 2 3 e ) + ( − 1 3 e ) 1p(+e)=2\times (\frac{2}{3}e)+(-\frac{1}{3}e) 1 p ( + e ) = 2 × ( 3 2 e ) + ( − 3 1 e )
1 n ( 0 ) = 2 × ( − 1 3 e ) + 2 3 e 1n(0)=2\times (-\frac{1}{3}e)+\frac{2}{3}e 1 n ( 0 ) = 2 × ( − 3 1 e ) + 3 2 e
25-3# F ⃗ = 1 4 π ε 0 ⋅ q 1 q 2 r 2 r ^ \vec F=\frac{1}{4\pi \varepsilon _0} \cdot \frac{q_1q_2}{r^2}\hat r F = 4 π ε 0 1 ⋅ r 2 q 1 q 2 r ^ Electrostatics in matter
Atom force H
Ionic Crystal force NaCl
Covalent Bond force H-H
Metal force Au
NOTE Coulomb’s laws an exact result for stationary
charges and not an approximation form some higher
law.
Gravitational vs Electric Force F e F g = 1 4 π ε 0 q 1 q 2 r 2 G m 1 m 2 r 2 = 4.17 × 1 0 42 \frac{F_e}{F_g}=\cfrac{\frac{1}{4\pi \varepsilon _0}\frac{q_1q_2}{r^2}}{G\frac{m_1m_2}{r^2}}=4.17\times 10^{42} F g F e = G r 2 m 1 m 2 4 π ε 0 1 r 2 q 1 q 2 = 4.17 × 1 0 42 e.g 25-3
for a man ,he push his arms apart with a force of 450N,how many charge can he hold outstretched?
F = 450 N Q = r F k = 4.47 × 1 0 − 4 F=450N\\ Q=r\sqrt{\frac{F}{k}}=4.47\times 10^{-4} F = 450 N Q = r k F = 4.47 × 1 0 − 4 e.g 25-3-2
How many electrons in a person by Feynman
treat people like water
λ p = N A M r ( H 2 O ) × e ( H 2 O ) = 3.3 × 1 0 23 e / g \lambda_p=\frac{NA}{M_r(H_2O)}\times e(H_2O)=3.3\times 10^{23}e/g λ p = M r ( H 2 O ) N A × e ( H 2 O ) = 3.3 × 1 0 23 e / g then ,assume he is 80kg
n e = λ p m = 2.6 × 1 0 28 e n_e=\lambda _p m=2.6\times 10^{28}e n e = λ p m = 2.6 × 1 0 28 e 1% of a person
1 % × 2.6 × 1 0 28 × 1.6 × 1 0 − 19 = 4.2 × 1 0 7 C 1\%\times 2.6\times 10^{28}\times 1.6\times 10^{-19}=4.2\times 10^7C 1% × 2.6 × 1 0 28 × 1.6 × 1 0 − 19 = 4.2 × 1 0 7 C then for two people 0.75m apart:
F = 9 × 1 0 9 × ( 4.2 × 1 0 7 C 0.75 m ) 2 = 2.8 × 1 0 25 ≈ W e a r t h = 6 × 1 0 24 k g × 9.8 m / s 2 F=9\times 10^{9}\times \left(\frac{4.2\times 10^7C}{0.75m}\right)^2=2.8\times 10^{25}\approx W_{earth}=6\times 10^{24}kg\times 9.8m/s^2 F = 9 × 1 0 9 × ( 0.75 m 4.2 × 1 0 7 C ) 2 = 2.8 × 1 0 25 ≈ W e a r t h = 6 × 1 0 24 k g × 9.8 m / s 2 IMPORTANT you should distinguish the difference between the vec and scalars
25-4 Conductors and Insulators# Insulators : ⩽ 1 e c p e r c m 3 \leqslant 1 e_c ~\mathrm{per}~ cm^3 ⩽ 1 e c per c m 3 Glass,Plastics,Dry wood Conductors : ≈ 1 0 23 e c p e r c m 3 \approx 10^{23} e_c ~\mathrm{per}~ cm^3 ≈ 1 0 23 e c per c m 3 Aluminum,Copper,Silver… Semiconductor : 1 0 10 → 1 0 12 p e r c m 3 10^{10}\to 10^{12} ~\mathrm{per}~ cm^3 1 0 10 → 1 0 12 per c m 3 Silicon,Germanium Superconductor : R = 0 , B = 0 R=0,B=0 R = 0 , B = 0 (the following picture is from OCR,so some fault occurred )
H g ( T c = 4.2 K , 1911 ) N h S n ( T c = 23 K , 1969 ) , Y B a 2 C u 3 O , ( T c = 90 K , 1987 ) H g B a C a C u O ( T c = 156 K , 1988 ) R e O 1 , F 2 F e e A 3 ( T c = 55 K , 2008 ) ( B a K ) F e 2 A s 2 , ( T c = 39 K , 2008 ) H 3 S ( T c = 210 K , H i g h P r e s s u r e , 2016 ) L a H 10 ( T c = 250 K , H i g h P r e s s u r e , 2019 ) P e ( T e , S o ) ( T c = 144 K , 2008 ) ( T i , K , R b , C S ) ) F e s ( S e s , ( T c = 30 K , 2010 ) . . . . . . . . . T h N i 2 S e 2 , T h N i 2 S 2 ( T c = 3.7 K , 2013 ) \begin{aligned}&\mathrm{Hg}\left(T_{c}{=}4.2K,1911\right)\\&\mathrm{NhSn}\left(T_{c}{=}23K,1969\right),\\&\mathrm{YBa}_{2}\mathrm{Cu}_{3}\mathrm{O},\quad(T_{c}{=}90K,1987)\\&\mathrm{HgBaCaCuO}\quad(T_{c}{=}156K,1988)\\&\mathrm{ReO}_{1},\mathrm{F}_{2}\mathrm{FeeA}_{3}\mathrm{~(T_{c}{=}55K,2008)}\\&\mathrm{(BaK)Fe}_{2}\mathrm{As}_{2},(T_{c}{=}39K,2008)\\&\mathrm{H}_{3}\mathrm{S}\quad(T_{c}{=}210\mathrm{K},\mathrm{High~Pressure},2016)\\&\mathrm{LaH}_{10}(T_{c}{=}250\mathrm{K},\mathrm{High~Pressure},2019)\\&\mathrm{Pe}(\mathrm{Te},\mathrm{So})\quad(T_{c}{=}144K,2008)\\&(\mathrm{Ti},\mathrm{K},\mathrm{Rb},\mathrm{CS}))\mathrm{Fe}_{s}(\mathrm{Se}_{s},\quad(T_{c}{=}30K,2010).........\\&\mathrm{ThNi}_{2}\mathrm{Se}_{2},\mathrm{ThNi}_{2}\mathrm{S}_{2}(T_{c}{=}3.7K,2013)\end{aligned} Hg ( T c = 4.2 K , 1911 ) NhSn ( T c = 23 K , 1969 ) , YBa 2 Cu 3 O , ( T c = 90 K , 1987 ) HgBaCaCuO ( T c = 156 K , 1988 ) ReO 1 , F 2 FeeA 3 ( T c = 55K , 2008 ) ( BaK ) Fe 2 As 2 , ( T c = 39 K , 2008 ) H 3 S ( T c = 210 K , High Pressure , 2016 ) LaH 10 ( T c = 250 K , High Pressure , 2019 ) Pe ( Te , So ) ( T c = 144 K , 2008 ) ( Ti , K , Rb , CS )) Fe s ( Se s , ( T c = 30 K , 2010 ) ......... ThNi 2 Se 2 , ThNi 2 S 2 ( T c = 3.7 K , 2013 ) NMR(Nuclear Magnetic Resonance ) Brain research **Magnetic Levitation **(Maglev) 25-5 Continuous Charge Distribution# The charge density
λ = d q d x \lambda =\frac{\mathrm d q}{\mathrm d x} λ = d x d q σ = d q d A \sigma =\frac{\mathrm d q}{\mathrm d A} σ = d A d q ρ = d q d V \rho =\frac{\mathrm d q}{\mathrm d V} ρ = d V d q to calculate q 0 → ( d i s t r i b u t i o n ) ρ q_0\to (\mathrm{distribution})\rho q 0 → ( distribution ) ρ
d F q 0 ⃗ = 1 4 π ε 0 q 0 ( ρ d V ) ∣ r ⃗ − r ⃗ ′ ∣ 3 ( r ⃗ − r ⃗ ′ ) \mathrm d\vec {F_{q_0}}=\frac{1}{4\pi \varepsilon _0}\frac{q_0(\rho \mathrm d V)}{|\vec r-\vec r'|^3} (\vec r-\vec r') d F q 0 = 4 π ε 0 1 ∣ r − r ′ ∣ 3 q 0 ( ρ d V ) ( r − r ′ ) eg-ring
For a uniform ring of charge :
λ = q 2 π R d F = 1 4 π ε 0 q 0 d q r 2 = 1 4 π ε 0 q 0 λ R d ϕ ( z 2 + R 2 ) F z = ∫ d F z = ∫ d F cos θ = ∫ 1 4 π ε 0 q 0 λ R d ϕ ( z 2 + R 2 ) z z 2 + R 2 = 1 4 π ε 0 q 0 λ R z ( z 2 + R 2 ) 3 / 2 ∫ 0 2 π d ϕ = 1 4 π ε 0 q 0 q z ( z 2 + R 2 ) 3 / 2 \begin{aligned} &\lambda=\frac{q}{2\pi R} \\ &dF=\frac{1}{4\pi\varepsilon_{0}}\frac{q_{0}dq}{r^{2}}=\frac{1}{4\pi\varepsilon_{0}}\frac{q_{0}\lambda Rd\phi}{(z^{2}+R^{2})} \\ &F_{z}=\int dF_{z}=\int dF\cos\theta \\ &=\int\frac1{4\pi\varepsilon_0}\frac{q_0\lambda Rd\phi}{(z^2+R^2)}\frac z{\sqrt{z^2+R^2}} \\ &=\frac1{4\pi\varepsilon_0}\frac{q_0\lambda Rz}{\left(z^2+R^2\right)^{3/2}}\int_0^{2\pi}d\phi \\ &=\frac1{4\pi\varepsilon_0}\frac{q_0qz}{\left(z^2+R^2\right)^{3/2}} \end{aligned} λ = 2 π R q d F = 4 π ε 0 1 r 2 q 0 d q = 4 π ε 0 1 ( z 2 + R 2 ) q 0 λ R d ϕ F z = ∫ d F z = ∫ d F cos θ = ∫ 4 π ε 0 1 ( z 2 + R 2 ) q 0 λ R d ϕ z 2 + R 2 z = 4 π ε 0 1 ( z 2 + R 2 ) 3/2 q 0 λ R z ∫ 0 2 π d ϕ = 4 π ε 0 1 ( z 2 + R 2 ) 3/2 q 0 q z for approximation
z → ∞ , F z → 1 4 π ε 0 q 0 q z 2 z\to \infty ,F_z\to \frac{1}{4\pi \varepsilon _0}\frac{q_0q}{z^2} z → ∞ , F z → 4 π ε 0 1 z 2 q 0 q eg-disk
For a uniform disk of charge :
σ = q π R 2 d q = σ d A = 2 π σ ω d ω d F z = 1 4 π ε 0 q 0 ( 2 π σ ω d ω ) ( z 2 + ω 2 ) 3 2 F z = 1 4 π ε 0 q 0 2 π σ z ∫ 0 R ω d ω ( z 2 + ω 2 ) 3 2 = 1 4 π ε 0 2 q 0 q R 2 ( 1 − z z 2 + R 2 ) \begin{aligned} \sigma &=\frac{q}{\pi R^2}\\\mathrm d q&=\sigma \mathrm dA =2\pi \sigma \omega \mathrm d\omega\\\mathrm dF_z&=\frac{1}{4\pi \varepsilon _0}\frac{q_0(2\pi \sigma \omega \mathrm d\omega)}{(z^2+\omega ^2)^{\frac{3}{2}}}\\F_z&=\frac{1}{4\pi \varepsilon _0}q_02\pi \sigma z \int _{0}^R \frac{\omega \mathrm d\omega }{(z^2+\omega ^2)^{\frac{3}{2}}}\\&=\frac{1}{4\pi \varepsilon _0 }\frac{2q_0q}{R^2}\left(1-\frac{z}{\sqrt{z^2+R^2}}\right) \end{aligned} σ d q d F z F z = π R 2 q = σ d A = 2 πσω d ω = 4 π ε 0 1 ( z 2 + ω 2 ) 2 3 q 0 ( 2 πσω d ω ) = 4 π ε 0 1 q 0 2 πσ z ∫ 0 R ( z 2 + ω 2 ) 2 3 ω d ω = 4 π ε 0 1 R 2 2 q 0 q ( 1 − z 2 + R 2 z ) for approximation
z → ∞ , F z → 1 4 π ε 0 q 0 q z 2 z\to \infty ,F_z\to \frac{1}{4\pi \varepsilon _0}\frac{q_0q}{z^2} z → ∞ , F z → 4 π ε 0 1 z 2 q 0 q 25-6 Charge conservation# e + + e − → 2 γ n → p + e − + ν e e^++e^{-}\to 2\gamma\\n\to p+e^- +\nu_e e + + e − → 2 γ n → p + e − + ν e Chap. 26 Electric Fields# 26-1 Field# Mass-field-mass: not action at a distance
26-2 E field# E ⃗ = lim q 0 → 0 F ⃗ q 0 \vec E=\lim _{q_0\to 0}\frac{\vec F}{q_0} E = q 0 → 0 lim q 0 F 26-3 The Electric field of point charge# we just deal with electrostatics instead of electrodynamics
for a single charge q q q
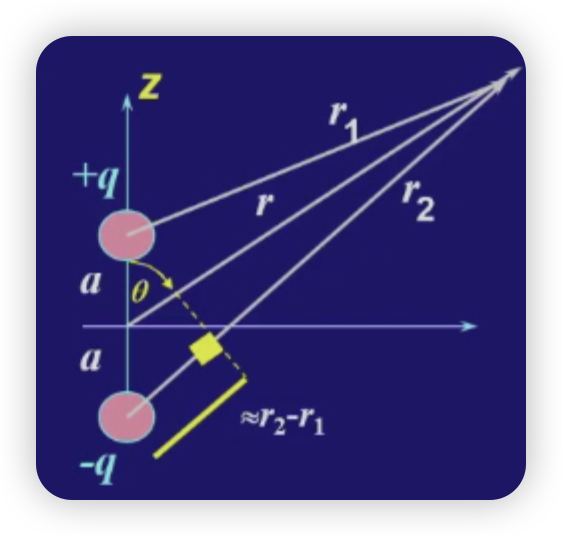
E ⃗ = F q 0 = 1 4 π ε 0 1 r 2 r ^ \vec E=\frac{F}{q_0}=\frac{1}{4\pi \varepsilon _0}\frac{1}{r^2}\hat r E = q 0 F = 4 π ε 0 1 r 2 1 r ^ for the Electric Dipole (p = 2 Q a = Q l p=2Qa=Ql p = 2 Q a = Ql
remember p ⃗ = q ⋅ l ⃗ \vec p=q\cdot\vec l p = q ⋅ l − q -q − q + q +q + q
E x ( x , 0 ) = 0 E y ( x , 0 ) = − 2 1 4 π ε 0 Q r 2 sin θ sin θ = a r , r = x 2 + a 2 E y ( x , 0 ) = − 2 1 4 π ε 0 Q a ( x 2 + a 2 ) 3 2 → − 2 k Q a r 3 E_x(x,0)=0\\E_y(x,0)=-2\frac{1}{4\pi \varepsilon _0}\frac{Q}{r^2}\sin \theta\\\sin \theta =\frac{a}{r},r=\sqrt{x^2+a^2}\\E_y(x,0)=-2\frac{1}{4\pi \varepsilon _0} \frac{Qa}{(x^2+a^2)^{\frac{3}{2}}}\to-2k\frac{Qa}{r^3} E x ( x , 0 ) = 0 E y ( x , 0 ) = − 2 4 π ε 0 1 r 2 Q sin θ sin θ = r a , r = x 2 + a 2 E y ( x , 0 ) = − 2 4 π ε 0 1 ( x 2 + a 2 ) 2 3 Q a → − 2 k r 3 Q a then for y-axis
E x ( 0 , r ) = 0 E y ( 0 , r ) = Q 4 π ε 0 4 a r r 4 ( 1 − a 2 r 2 ) 2 → E y ( 0 , r ) ≈ + 4 1 4 π ε 0 Q a r 3 = 4 k Q a r 3 E_x\left(0,r\right)=0\\E_y(0,r)=\frac{Q}{4\pi\varepsilon_0}\frac{4ar}{r^4\left(1-\frac{a^2}{r^2}\right)^2}\to E_y(0,r)\approx+4\frac1{4\pi\varepsilon_0}\frac{Qa}{r^3}=4k\frac{Qa}{r^3} E x ( 0 , r ) = 0 E y ( 0 , r ) = 4 π ε 0 Q r 4 ( 1 − r 2 a 2 ) 2 4 a r → E y ( 0 , r ) ≈ + 4 4 π ε 0 1 r 3 Q a = 4 k r 3 Q a NaCl e.g.
2 a = 0.236 n m , p t = 2 e a = 1.6 × 3.78 × 1 0 − 29 2a=0.236nm,p_t=2ea=1.6\times 3.78\times 10^{-29} 2 a = 0.236 nm , p t = 2 e a = 1.6 × 3.78 × 1 0 − 29
p e = 3 × 1 0 − 29 p_e=3\times 10^{-29} p e = 3 × 1 0 − 29
it indicates that the electron is not entirely removed from Na to Cl
for x > > a x>>a x >> a
we can approximate E E E
E = p k x 3 [ 1 + ( − 3 2 ) ( a x ) 2 + ⋯ ] ∝ 1 r 3 E=\frac{pk}{x^3}[1+(-\frac{3}{2})(\frac{a}{x})^2+\cdots ]\propto \frac{1}{r^3} E = x 3 p k [ 1 + ( − 2 3 ) ( x a ) 2 + ⋯ ] ∝ r 3 1 26-4 The Electric field of Continuous Charge Distribution# once again we turn to distribution densities:d q = λ d x = σ d A = ρ d V \mathrm d q=\lambda d x=\sigma d A=\rho d V d q = λ d x = σ d A = ρ d V
d E x = − 1 4 π ε 0 λ d θ r sin θ d E y = + 1 4 π ε 0 λ d θ r cos θ dE_{x}=-\frac{1}{4\pi\varepsilon_{0}}\frac{\lambda d\theta}{r}\sin\theta\\dE_{y}=+\frac{1}{4\pi\varepsilon_{0}}\frac{\lambda d\theta}{r}\cos\theta d E x = − 4 π ε 0 1 r λ d θ sin θ d E y = + 4 π ε 0 1 r λ d θ cos θ then
E x = 0 , E y = ∫ − π 2 π 2 k λ d θ r cos θ = 2 k λ r = λ 2 π ε 0 r ∝ 1 r E_x=0,E_y=\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}} k \frac{\lambda \mathrm d \theta}{r}\cos \theta =\frac{2k\lambda}{r}=\frac{\lambda}{2\pi \varepsilon _0 r}\propto \frac{1}{r} E x = 0 , E y = ∫ − 2 π 2 π k r λ d θ cos θ = r 2 kλ = 2 π ε 0 r λ ∝ r 1
d E = λ d s 4 π ε 0 r 2 = λ d s 4 π ε 0 ( z 2 + R 2 ) d E z = d E cos θ = λ d s 4 π ε 0 ( z 2 + R 2 ) ⋅ z ( z 2 + R 2 ) 1 / 2 = z λ d s 4 π ε 0 ( z 2 + R 2 ) 3 / 2 E z = z 4 π ε 0 ( z 2 + R 2 ) 3 2 ∫ 0 2 π R λ d s → q 4 π ε 0 z 2 \begin{aligned} &dE=\frac{\lambda ds}{4\pi\varepsilon_{0}r^{2}}=\frac{\lambda ds}{4\pi\varepsilon_{0}(z^{2}+R^{2})} \\ &dE_{z}=dE\cos\theta \\ &=\frac{\lambda ds}{4\pi\varepsilon_{0}(z^{2}+R^{2})}\cdot\frac{z}{(z^{2}+R^{2})^{1/2}} \\ &=\frac{z\lambda ds}{4\pi\varepsilon_0(z^2+R^2)^{3/2}}\\E_z&=\frac{z}{4\pi \varepsilon _0(z^2+R^2)^{\frac{3}{2}}}\int _{0}^{2\pi R}\lambda \mathrm ds\to \frac{q}{4\pi \varepsilon _0z^2} \end{aligned} E z d E = 4 π ε 0 r 2 λ d s = 4 π ε 0 ( z 2 + R 2 ) λ d s d E z = d E cos θ = 4 π ε 0 ( z 2 + R 2 ) λ d s ⋅ ( z 2 + R 2 ) 1/2 z = 4 π ε 0 ( z 2 + R 2 ) 3/2 z λ d s = 4 π ε 0 ( z 2 + R 2 ) 2 3 z ∫ 0 2 π R λ d s → 4 π ε 0 z 2 q
d q = 2 π ω ⋅ d ω ⋅ σ d E = z d q 4 π ε 0 ( z 2 + ω 2 ) 3 / 2 = z 2 π σ ω d ω 4 π ε 0 ( z 2 + ω 2 ) 3 / 2 E = ∫ d E = σ z 2 ε 0 ∫ 0 R ω d ω ( z 2 + ω 2 ) 3 / 2 = σ z 4 ε 0 ∫ 0 R d ( z 2 + ω 2 ) ( z 2 + ω 2 ) 3 / 2 = σ 2 ε 0 ( 1 − 1 1 + R 2 z 2 ) R > > z : E → σ 2 ε 0 z > > R : E = σ 2 ε 0 ( 1 2 ( R z ) 2 − 3 8 ( R z ) 4 + ⋯ ) → q 4 π ε 0 z 2 \begin{aligned} &dq=2\pi\omega\cdot d\omega\cdot\sigma \\ &dE=\frac{zdq}{4\pi\varepsilon_{0}(z^{2}+\omega^{2})^{3/2}}=\frac{z2\pi\sigma\omega d\omega}{4\pi\varepsilon_{0}(z^{2}+\omega^{2})^{3/2}} \\ &E=\int dE=\frac{\sigma z}{2\varepsilon_{0}}\int_{0}^{R}\frac{\omega d\omega}{\left(z^{2}+\omega^{2}\right)^{3/2}} \\ &=\frac{\sigma z}{4\varepsilon_{0}}\int_{0}^{R}\frac{d(z^{2}+\omega^{2})}{(z^{2}+\omega^{2})^{3/2}} \\ &=\frac{\sigma}{2\varepsilon_{0}}(1-\frac{1}{\sqrt{1+\frac{R^{2}}{z^{2}}}})\\&R>>z:E\to \frac{\sigma }{2\varepsilon_0}\\&z>>R:E=\frac{\sigma }{2\varepsilon _0}\left(\frac{1}{2}\left(\frac{R}{z}\right)^2-\frac{3}{8}\left(\frac{R}{z}\right)^4+\cdots\right)\to \frac{q}{4\pi \varepsilon _0 z^2} \end{aligned} d q = 2 πω ⋅ d ω ⋅ σ d E = 4 π ε 0 ( z 2 + ω 2 ) 3/2 z d q = 4 π ε 0 ( z 2 + ω 2 ) 3/2 z 2 πσω d ω E = ∫ d E = 2 ε 0 σ z ∫ 0 R ( z 2 + ω 2 ) 3/2 ω d ω = 4 ε 0 σ z ∫ 0 R ( z 2 + ω 2 ) 3/2 d ( z 2 + ω 2 ) = 2 ε 0 σ ( 1 − 1 + z 2 R 2 1 ) R >> z : E → 2 ε 0 σ z >> R : E = 2 ε 0 σ ( 2 1 ( z R ) 2 − 8 3 ( z R ) 4 + ⋯ ) → 4 π ε 0 z 2 q Summary# when r > > a / R r>>a/R r >> a / R
Dipole p = 2 Q a = Q l p=2Qa=Ql p = 2 Q a = Ql
in line : E = 4 Q a 4 π ε 0 r 3 = 2 p 4 π ε 0 r 3 E=\frac{4Qa}{4\pi \varepsilon_0 r^3 }=\frac{2p}{4\pi \varepsilon _0r^3} E = 4 π ε 0 r 3 4 Q a = 4 π ε 0 r 3 2 p off line : E = 2 Q a 4 π ε 0 r 3 = p 4 π ε 0 r 3 E=\frac{2Qa}{4\pi \varepsilon _0r^3}=\frac{p}{4\pi \varepsilon _0r^3} E = 4 π ε 0 r 3 2 Q a = 4 π ε 0 r 3 p Point E = q 4 π ε 0 r 2 E=\frac{q}{4\pi \varepsilon_0 r^2 } E = 4 π ε 0 r 2 q
Line E = 2 λ 4 π ϵ 0 r E=\frac{2\lambda }{4\pi \epsilon_0 r} E = 4 π ϵ 0 r 2 λ
Ring E = q 4 π ε 0 z 2 E=\frac{q}{4\pi \varepsilon _0z^2} E = 4 π ε 0 z 2 q
Disk E = q 4 π ε 0 z 2 E=\frac{q}{4\pi \varepsilon _0z^2} E = 4 π ε 0 z 2 q
26-5 E-Field Lines# { E x = E r sin θ cos ϕ E y = E r sin θ sin ϕ E z = E r cos θ \begin{cases}E_x=E_r\sin\theta\cos\phi\\E_y=E_r\sin\theta\sin\phi\\E_z=E_r\cos\theta\end{cases} ⎩ ⎨ ⎧ E x = E r sin θ cos ϕ E y = E r sin θ sin ϕ E z = E r cos θ 26-6 Point Charge in E-field# deflecting electrode system of an ink-jet printer
An ink drop : m = 1.3 × 1 0 − 10 k g L = 1.6 c m q = − 1.5 × l 0 − 13 C , E = 1.4 × 1 0 6 N / C v = 18 m / s \begin{aligned}\text{An ink drop}&:m=1.3\times 10^{-10}kg\quad L=1.6cm\\&q=-1.5\times l0^{-13}C,\quad E=1.4\times 10^6N/C\\&v=18m/s\end{aligned} An ink drop : m = 1.3 × 1 0 − 10 k g L = 1.6 c m q = − 1.5 × l 0 − 13 C , E = 1.4 × 1 0 6 N / C v = 18 m / s y = 1 2 q E m L 2 v 2 ≈ 0.64 m m y=\frac{1}{2}\frac{qE}{m}\frac{L^2}{v^2}\approx 0.64mm y = 2 1 m qE v 2 L 2 ≈ 0.64 mm one letter -> about 100 drops
100000 drops/s → 1000 \to 1000 → 1000
bonus
the elementary charge
e = 1.602 × 1 0 − 19 C e=1.602\times 10^{-19}C e = 1.602 × 1 0 − 19 C skip
then in an ununiformed field,for example
F = q E ≠ c o n s t F ( z ) d 2 z d t 2 = q m E ( z ) E = Q z 4 π ε 0 ( z 2 + R 2 ) 3 / 2 d 2 z d t 2 = q m Q z 4 π ε 0 ( z 2 + R 2 ) 3 / 2 \begin{aligned} &F=qE\neq const\quad F(z) \\ &\frac{d^{2}z}{dt^{2}}=\frac{q}{m}E(z) \\ &E=\frac{\mathrm{Q}z}{4\pi\varepsilon_{0}(z^{2}+R^{2})^{3/2}} \\ &\frac{d^{2}z}{dt^{2}}=\frac{q}{m}\frac{Qz}{4\pi\varepsilon_{0}(z^{2}+R^{2})^{3/2}} \end{aligned} F = qE = co n s t F ( z ) d t 2 d 2 z = m q E ( z ) E = 4 π ε 0 ( z 2 + R 2 ) 3/2 Q z d t 2 d 2 z = m q 4 π ε 0 ( z 2 + R 2 ) 3/2 Q z 26-7 Dipole in E-field#
Torque:τ ⃗ = p E sin θ = p ⃗ × E ⃗ \vec \tau=pE\sin \theta=\vec p\times \vec E τ = pE sin θ = p × E W = ∫ θ 0 θ = p E ( cos θ − cos θ 0 ) = − Δ U , U ( θ ) = − p ⃗ ⋅ E ⃗ W=\int _{\theta_0}^\theta =pE(\cos \theta -\cos \theta_0)=-\Delta U,U(\theta)=-\vec p\cdot \vec E W = ∫ θ 0 θ = pE ( cos θ − cos θ 0 ) = − Δ U , U ( θ ) = − p ⋅ E we can divide molecules to
Dipole-molecule H 2 O \mathrm{H_2O} H 2 O non-dipole molecule C 2 O \mathrm{C_2O} C 2 O the max torque on H2O
τ = q E sin θ = 9.3 × 1 0 − 26 N ⋅ m θ : π → 0 : W = 2 p E = 1.9 × 1 0 − 25 J ϵ i n t = 3 k T 2 − 6.3 × 1 0 − 21 > > ϵ e l e c t \tau =qE\sin \theta =9.3\times 10^{-26}N\cdot m\\ \\ \theta :\pi\to 0 :W=2pE=1.9\times 10^{-25}J\\ \epsilon _{int}=\frac{3kT}{2}-6.3\times 10^{-21}>>\epsilon _{elect} τ = qE sin θ = 9.3 × 1 0 − 26 N ⋅ m θ : π → 0 : W = 2 pE = 1.9 × 1 0 − 25 J ϵ in t = 2 3 k T − 6.3 × 1 0 − 21 >> ϵ e l ec t 26-8 Atom Nuclear Model# Thomson model plum pudding Rutherford:
E max = Q 4 π ε 0 R 2 = 1.2 × 1 0 13 N / C R = 1.0 × 1 0 − 10 m Q = 79 e U = 6 M e v = 9.6 × 1 0 − 13 J ν = 2 U m = 1.7 × 1 0 7 m / s \begin{aligned} &E_{\max}=\frac{Q}{4\pi\varepsilon_{0}R^{2}}=1.2\times10^{13}N/C \\ &R=1.0\times10^{-10}m \\ &Q=79e \\ &U=6\mathrm{Mev}=9.6\times10^{-13}J \\ &\nu=\sqrt{\frac{2U}{m}}=1.7\times10^{7}m/s \end{aligned} E m a x = 4 π ε 0 R 2 Q = 1.2 × 1 0 13 N / C R = 1.0 × 1 0 − 10 m Q = 79 e U = 6 Mev = 9.6 × 1 0 − 13 J ν = m 2 U = 1.7 × 1 0 7 m / s F = q E max = m a a = q m E max Δ ν = a Δ t = q m E max 2 R ν = 6.6 × 1 0 3 m / s ∴ θ = t g − 1 Δ ν ν = t g − 1 ( 6.6 × 1 0 3 1.7 × 1 0 7 ) ≈ 0.02 \begin{aligned} &F=qE_{\max}=ma \\ &a=\frac{q}{m}E_{\max} \\ &\Delta\nu=a\Delta t=\frac{q}{m}E_{\max}\frac{2R}{\nu}=6.6\times10^{3}m/s \\ &\therefore\theta=tg^{-1}\frac{\Delta\nu}{\nu}=tg^{-1}(\frac{6.6\times10^{3}}{1.7\times10^{7}})\approx0.02 \end{aligned} F = q E m a x = ma a = m q E m a x Δ ν = a Δ t = m q E m a x ν 2 R = 6.6 × 1 0 3 m / s ∴ θ = t g − 1 ν Δ ν = t g − 1 ( 1.7 × 1 0 7 6.6 × 1 0 3 ) ≈ 0.02 then , the result disobeys the experimental result!
Chap. 27 Gauss Law# 27-2(3) Flux# We need to at first define flux and the vector of surface of a closed region.
Φ = ∮ ν ⃗ ∙ d A ⃗ d Φ = ν ⃗ ∙ d A ⃗ d A ⃗ = d y d z i ⃗ + d z d x j ⃗ + d x d y k ⃗ ν ⃗ = ν x i ⃗ + ν y j ⃗ + ν z k ⃗ ν ⃗ • d A ⃗ = ν x d y d z + ν y d z d x + ν z d x d y \begin{aligned} &\Phi=\oint\vec{\nu}\bullet d\vec{A} \\ &d\Phi=\vec{\nu}\bullet d\vec{A} \\ &d\vec{A}=dydz\vec{i}+dzdx\vec{j}+dxdy\vec{k} \\ &\vec{\nu}=\nu_{x}\vec{i}+\nu_{y}\vec{j}+\nu_{z}\vec{k} \\ &\vec{\nu}•d\vec{A}=\nu_{x}dydz+\nu_{y}dzdx+\nu_{z}dxdy \end{aligned} Φ = ∮ ν ∙ d A d Φ = ν ∙ d A d A = d y d z i + d z d x j + d x d y k ν = ν x i + ν y j + ν z k ν • d A = ν x d y d z + ν y d z d x + ν z d x d y if no source or sink of fluid
Φ = ∮ ν ⃗ ⋅ d A ⃗ = 0 \Phi=\oint \vec \nu \cdot \mathrm d\vec A=0 Φ = ∮ ν ⋅ d A = 0 for electrostatic case
Φ = ∮ E ⃗ ∙ d A ⃗ = q e n c l o s e d ε 0 \Phi=\oint\vec{E}\bullet \mathrm d\vec{A}=\frac{q_{enclosed}}{\varepsilon _0} Φ = ∮ E ∙ d A = ε 0 q e n c l ose d Geometry and Surface Integrals# we can illustrate that Gauss’s Law -> Coulomb’s Law
for a +Q sphere having radius R R R
E ⋅ 4 π R 2 = Q ε 0 E \cdot 4\pi R^2=\frac{Q}{\varepsilon _0} E ⋅ 4 π R 2 = ε 0 Q
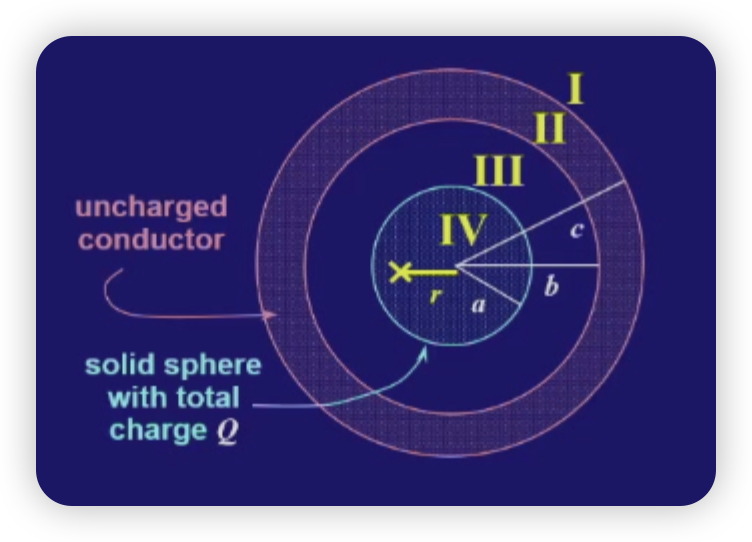
27-5(6) Application Gauss’s Law# Uniform charged sphere
q = 4 3 π a 3 ρ ⇒ E = ρ a 3 3 ε 0 r 2 ( r > a ) E = ρ r 3 ε 0 ( r < a ) q=\frac{4}{3}\pi a^3\rho\Rightarrow E=\frac{\rho a^3}{3\varepsilon _0r^2}(r>a)\\E=\frac{\rho r}{3\varepsilon _0}(r<a) q = 3 4 π a 3 ρ ⇒ E = 3 ε 0 r 2 ρ a 3 ( r > a ) E = 3 ε 0 ρ r ( r < a ) since E=0 inside a conductor Q i n s i d e = 0 Q_{inside}=0 Q in s i d e = 0
For a conductor,we obtain a cylinder gauss plane:
ε 0 E Δ A + 0 + 0 = σ Δ A E = σ ε 0 \varepsilon_0E\Delta A+0+0=\sigma \Delta A\\E=\frac{\sigma}{\varepsilon _0} ε 0 E Δ A + 0 + 0 = σ Δ A E = ε 0 σ Line——Cylindrical Symmetry# E ⋅ 2 π r h ⋅ ε 0 = λ h → E = λ 2 π ε 0 r E \cdot 2\pi r h\cdot \varepsilon_0=\lambda h\to E=\frac{ \lambda }{2\pi \varepsilon _0 r} E ⋅ 2 π r h ⋅ ε 0 = λh → E = 2 π ε 0 r λ Chap27,ACT2
Aline charge λ ( C/m ) \lambda\left(\text{C/m}\right) λ ( C/m ) r i = a r_i=a r i = a r o = b r_o=b r o = b
we need to get σ o \sigma_o σ o
TIP E o = λ 2 π ε 0 r = σ 0 b ε 0 r ⇒ σ o = λ 2 π b E_o=\frac{\lambda }{2\pi \varepsilon _0 r}=\frac{\sigma_0b}{\varepsilon _0 r}\Rightarrow \sigma_o=\frac{\lambda}{2\pi b} E o = 2 π ε 0 r λ = ε 0 r σ 0 b ⇒ σ o = 2 πb λ Sheets——Planar Symmetry# ε 0 ( 2 E A ) = σ A ⇒ E = σ 2 ε 0 \varepsilon _0(2EA)=\sigma A \Rightarrow E=\frac{\sigma}{2\varepsilon _0} ε 0 ( 2 E A ) = σ A ⇒ E = 2 ε 0 σ for two paralleled sheets
E i n = σ ε 0 E_{in}=\frac{\sigma}{\varepsilon _0} E in = ε 0 σ
E A = − σ 1 2 ε 0 E B = + σ 1 2 ε 0 E C = 0 E D = + σ 1 2 ε 0 E_A=\frac{-\sigma_1}{2\varepsilon _0}\\E_B=\frac{+\sigma_1}{2\varepsilon _0}\\E_C=0\\E_D=\frac{+\sigma_1}{2\varepsilon _0} E A = 2 ε 0 − σ 1 E B = 2 ε 0 + σ 1 E C = 0 E D = 2 ε 0 + σ 1 always based on gauss plane
Q 2 = − 3 Q 1 Q_2=-3Q_1 Q 2 = − 3 Q 1 σ i = − Q 1 4 π R 2 2 σ o = − 2 Q 1 4 π R 2 2 E = { 0 r < R 1 1 4 π ε 0 Q 1 r 2 R 1 < r < R 2 − 1 4 π ε 0 2 Q 1 r 2 r > R 2 \sigma _i=-\frac{Q_1}{4\pi R_2^2}\\\sigma _o=-\frac{2Q_1}{4\pi R_2^2}\\E=\begin{cases}0&r<R_1\\\frac{1}{4\pi \varepsilon_0 }\frac{Q_1}{r^2} &R_1<r<R_2\\-\frac{1}{4\pi \varepsilon _0 }\frac{2Q_1}{r^2}&r>R_2\end{cases} σ i = − 4 π R 2 2 Q 1 σ o = − 4 π R 2 2 2 Q 1 E = ⎩ ⎨ ⎧ 0 4 π ε 0 1 r 2 Q 1 − 4 π ε 0 1 r 2 2 Q 1 r < R 1 R 1 < r < R 2 r > R 2 Once we connect the two spheres with a wire:,it becomes a whole conductor with − 2 Q 1 -2Q_1 − 2 Q 1
eg2 Cylinders
σ i = − λ 2 π R , σ o = σ t + λ 2 π R \sigma _i =-\frac{\lambda }{2\pi R},\sigma _o = \sigma_t+\frac{\lambda }{2\pi R} σ i = − 2 π R λ , σ o = σ t + 2 π R λ E r = { λ 2 π ε 0 r r < R λ 2 π ε 0 , r + σ R ε 0 r r > R E_r=\begin{cases}\frac{\lambda }{2\pi \varepsilon _0 r}&r<R\\\frac{\lambda }{2\pi \varepsilon _0,r}+\frac{\sigma R}{\varepsilon _0r} &r>R\end{cases} E r = { 2 π ε 0 r λ 2 π ε 0 , r λ + ε 0 r σ R r < R r > R 27-7 Experimental Tests of Gauss’ Law and Coulomb’s Law# WARNING just skip
Chap. 28 Electric Potential U & V# 28-1 Potential Energy#
The union energy of two points of charge :
U b − U a = − W a , b = − ∫ a b F ⃗ ⋅ d l ⃗ U_b-U_a=-W_{a,b}=-\int_{a}^b \vec F\cdot \mathrm d\vec l U b − U a = − W a , b = − ∫ a b F ⋅ d l The circuit Law of electrostatics field# ∮ E ⃗ ⋅ d l ⃗ = 0 ∇ × E ⃗ = 0 \oint \vec E\cdot \mathrm d\vec l =0\\\nabla \times \vec E=0 ∮ E ⋅ d l = 0 ∇ × E = 0 The gauss’ law(the same as Math Analysis ):
∮ E ⃗ ⋅ d A ⃗ = q ε 0 = ∭ ρ ε 0 d V \oint \vec E\cdot\mathrm d \vec A =\frac{q}{\varepsilon _0}=\iiint \frac{\rho}{\varepsilon_0} \mathrm d V ∮ E ⋅ d A = ε 0 q = ∭ ε 0 ρ d V 28-2 Electric Potential# V p = U p q 0 V_p=\frac{U_p}{q_0} V p = q 0 U p V B − V A ≡ W A B q 0 = − ∫ A B E ⃗ ⋅ d l ⃗ V_B-V_A\equiv \frac{W_{AB}}{q_0}=-\int _{A}^B \vec E\cdot \mathrm d \vec l V B − V A ≡ q 0 W A B = − ∫ A B E ⋅ d l 28-3 Calculate Potential from E# W a b = − ∫ a b E ⃗ ⋅ d l ⃗ V p = W ∞ p = − ∫ ∞ p E ⃗ ⋅ d l ⃗ W_{ab}=-\int _{a}^b \vec E \cdot \mathrm d \vec l\\V_p=W_{\infty p}=-\int_{\infty}^{p} \vec E\cdot \mathrm d \vec l W ab = − ∫ a b E ⋅ d l V p = W ∞ p = − ∫ ∞ p E ⋅ d l for a point charge:
V b − V a = − ∫ r a r b q 4 π ε 0 r 2 d r = q 4 π ε 0 ( 1 r b − 1 r a ) V_b-V_a=-\int _{r_a}^{r_b}\frac{q}{4\pi \varepsilon _0r^2}\mathrm dr=\frac{q}{4\pi \varepsilon _0}\left(\frac{1}{r_b}-\frac{1}{r_a}\right) V b − V a = − ∫ r a r b 4 π ε 0 r 2 q d r = 4 π ε 0 q ( r b 1 − r a 1 ) Dipole
r > > a V r = 1 4 π ε 0 r 2 − r 1 r 1 r 2 r 2 − r 1 ≈ 2 a cos θ , r 1 r 2 = r 2 V r = 1 4 π ε 0 2 a q cos θ r 2 = p ⃗ ⋅ r ^ 4 π ε 0 r 2 r>>a\\V_r=\frac{1}{4\pi \varepsilon _0}\frac{r_2-r_1}{r_1r_2}\\ r_2-r_1\approx 2a\cos \theta ,r_1r_2=r^2\\ V_r=\frac{1}{4\pi \varepsilon_0}\frac{2aq\cos \theta }{r^2}=\frac{\vec p\cdot \hat r}{4\pi \varepsilon_0 r^2} r >> a V r = 4 π ε 0 1 r 1 r 2 r 2 − r 1 r 2 − r 1 ≈ 2 a cos θ , r 1 r 2 = r 2 V r = 4 π ε 0 1 r 2 2 a q cos θ = 4 π ε 0 r 2 p ⋅ r ^ quadrupole
V ( r ) = ∑ i V i ( r i ) = 1 4 π ε 0 ( q r − d + − 2 q r + q r + d ) = 1 4 π ε 0 2 q d 2 r ( r 2 − d 2 ) = 1 4 π ε 0 2 q d 2 r 3 ( 1 − d 2 / r 2 ) → Q 4 π ε 0 r 3 ( d < < r ) \begin{aligned} &V(r)=\sum_{i}V_{i}(r_{i}) \\ &=\frac{1}{4\pi\varepsilon_{0}}(\frac{q}{r-d}+\frac{-2q}{r}+\frac{q}{r+d}) \\ &=\frac{1}{4\pi\varepsilon_{0}}\frac{2qd^{2}}{r(r^{2}-d^{2})} \\ &=\frac{1}{4\pi\varepsilon_{0}}\frac{2qd^{2}}{r^{3}(1-d^{2}/r^{2})}\to \frac{Q}{4\pi \varepsilon _0r^3}(d<<r) \end{aligned} V ( r ) = i ∑ V i ( r i ) = 4 π ε 0 1 ( r − d q + r − 2 q + r + d q ) = 4 π ε 0 1 r ( r 2 − d 2 ) 2 q d 2 = 4 π ε 0 1 r 3 ( 1 − d 2 / r 2 ) 2 q d 2 → 4 π ε 0 r 3 Q ( d << r ) Point charge ∝ 1 r \propto \frac{1}{r} ∝ r 1 Dipole ∝ 1 r 2 \propto \frac{1}{r^2} ∝ r 2 1 Quadrupole ∝ 1 r 3 \propto \frac{1}{r^3} ∝ r 3 1 we can trace back to the distribution reflected by n-dipoles.
egs for potential calculation
for a charged sphere shell
E = [ r ⩾ R ] ⋅ q 4 π ε 0 r 2 E=[r\geqslant R]\cdot \frac{q}{4\pi \varepsilon _0r^2} E = [ r ⩾ R ] ⋅ 4 π ε 0 r 2 q V ( P ) = q 4 π ε 0 max { r P , R } V(P)=\frac{q}{4\pi \varepsilon _0\max \{r_P,R\}} V ( P ) = 4 π ε 0 max { r P , R } q U = 1 2 ∫ V d q = q 2 8 π ε 0 R U=\frac{1}{2} \int V\mathrm d q=\frac{q^2}{8\pi \varepsilon _0 R} U = 2 1 ∫ V d q = 8 π ε 0 R q 2 W = m c 2 = e 2 8 π ε 0 R ⇒ R e ≈ 1.4 × 1 0 − 15 m W=mc^2=\frac{e^2}{8\pi \varepsilon _0R}\Rightarrow R_e\approx 1.4\times 10^{-15}m W = m c 2 = 8 π ε 0 R e 2 ⇒ R e ≈ 1.4 × 1 0 − 15 m for a ring
V = ∮ 1 4 π ε 0 λ d s z 2 + R 2 = q 4 π ε 0 z 2 + R 2 V=\oint \frac{1}{4\pi \varepsilon _0}\frac{\lambda \mathrm d s}{\sqrt{z^2+R^2}}=\frac{q}{4\pi \varepsilon _0 \sqrt{z^2+R^2}} V = ∮ 4 π ε 0 1 z 2 + R 2 λ d s = 4 π ε 0 z 2 + R 2 q for a disk
d q = 2 π ω ⋅ d ω ⋅ σ d V = 2 π ω ⋅ d ω ⋅ σ 4 π ε 0 z 2 + ω 2 V = ∫ 0 R 2 π ω ⋅ d ω ⋅ σ 4 π ε 0 z 2 + ω 2 = σ 2 ε 0 ( z 2 + R 2 − z ) → q 4 π ε 0 z \begin{aligned} &dq=2\pi\omega\cdot d\omega\cdot\sigma \\ &dV=\frac{2\pi\omega\cdot d\omega\cdot\sigma}{4\pi\varepsilon_{0}\sqrt{z^{2}+\omega^{2}}} \\ &V=\int_{0}^{R}\frac{2\pi\omega\cdot d\omega\cdot\sigma}{4\pi\varepsilon_{0}\sqrt{z^{2}+\omega^{2}}}=\frac{\sigma}{2\varepsilon_{0}}(\sqrt{z^{2}+R^{2}}-z)\to \frac{q}{4\pi \varepsilon _0 z} \end{aligned} d q = 2 πω ⋅ d ω ⋅ σ d V = 4 π ε 0 z 2 + ω 2 2 πω ⋅ d ω ⋅ σ V = ∫ 0 R 4 π ε 0 z 2 + ω 2 2 πω ⋅ d ω ⋅ σ = 2 ε 0 σ ( z 2 + R 2 − z ) → 4 π ε 0 z q Sparks# High electric fields can ionize nonconducting materials(dielectrics )
(Insulator->Conductor)
ball breakdown
we have two ball shell with same potential V V V
Ball 2 is as twice large as Ball 1
as V V V
E s = Q 4 π ε 0 r 2 , V = Q 4 π ε 0 r ⇒ E = V r E_s=\frac{Q}{4\pi \varepsilon _0 r^2},V=\frac{Q}{4\pi \varepsilon_0 r}\Rightarrow E=\frac{V}{r} E s = 4 π ε 0 r 2 Q , V = 4 π ε 0 r Q ⇒ E = r V then r 1 < r 2 ⇒ E 1 > E 2 r_1<r_2\Rightarrow E_1>E_2 r 1 < r 2 ⇒ E 1 > E 2
Δ V > 0 \Delta V>0 Δ V > 0 Δ V < 0 \Delta V<0 Δ V < 0 V ( r ) = V ∞ − ∫ ∞ c E ⃗ l ⋅ l ⃗ − ∫ c b E ⃗ l ⋅ l ⃗ − ∫ b a E ⃗ l ⋅ l ⃗ − ∫ a r E ⃗ l ⋅ l ⃗ = V ∞ − ( ∫ ∞ c + ∫ b a ) 1 4 π ε 0 Q r 2 d r − ∫ a r 1 4 π ε 0 Q r a 3 d r = Q 4 π ε 0 ( 1 a − ( 1 b − 1 c ) + 1 2 a ( 1 − r 2 a 2 ) ) V(r)=V_\infty -\int_{\infty}^c \vec E_l\cdot \vec l-\int_{c}^b \vec E_l\cdot \vec l-\int_{b}^a \vec E_l\cdot \vec l-\int_{a}^r \vec E_l\cdot \vec l\\=V_\infty-\left(\int _{\infty}^c+\int_{b}^{a}\right )\frac{1}{4\pi \varepsilon _0}\frac{Q}{r^2}\mathrm dr-\int_{a}^r \frac{1}{4\pi\varepsilon _0}\frac{Qr}{a^3}\mathrm dr\\=\frac{Q}{4\pi \varepsilon _0}\left(\frac{1}{a}-\left(\frac{1}{b}-\frac{1}{c}\right)+\frac{1}{2a}\left(1-\frac{r^2}{a^2}\right)\right) V ( r ) = V ∞ − ∫ ∞ c E l ⋅ l − ∫ c b E l ⋅ l − ∫ b a E l ⋅ l − ∫ a r E l ⋅ l = V ∞ − ( ∫ ∞ c + ∫ b a ) 4 π ε 0 1 r 2 Q d r − ∫ a r 4 π ε 0 1 a 3 Q r d r = 4 π ε 0 Q ( a 1 − ( b 1 − c 1 ) + 2 a 1 ( 1 − a 2 r 2 ) ) you can split into two patterns
28-4 Equipotentials# when in the equipotential surface we can conclude
E ⃗ ⋅ d l ⃗ ≡ V \vec E\cdot \mathrm d\vec l\equiv V E ⋅ d l ≡ V 28-5 Potential of a charged conductors# IMPORTANT Claim: The surface of a conductor is an equipotential surfacewhen two sphere conductors are attatched to each others.
Q A Q B = r A r B \frac{Q_A}{Q_B}=\frac{r_A}{r_B} Q B Q A = r B r A for example , when a point of charge is placed off-center inside a sphere conductor,the inside surface will be inuniform and the outside surface will be uniform
28-6 Calculate E from Potential# V P = ∫ P ∞ E ⃗ ⋅ d l ⃗ V_P=\int _{P}^{\infty }\vec E\cdot \mathrm d \vec l V P = ∫ P ∞ E ⋅ d l eg
V = 3 x 2 + 2 x y − z 2 E ⃗ = ( − 6 x − 2 y , − 2 x , 2 z ) T E ⃗ = 2 a q 4 π ε 0 r 3 ( 2 cos θ , sin θ , 0 ) s p T \begin{align*} V=3x^2+2xy-z^2 \\ \vec E=(-6x-2y,-2x,2z)^T\\ \vec E=\frac{2aq}{4\pi \varepsilon _0r^3}(2\cos \theta ,\sin \theta ,0)_{sp}^T \end{align*} V = 3 x 2 + 2 x y − z 2 E = ( − 6 x − 2 y , − 2 x , 2 z ) T E = 4 π ε 0 r 3 2 a q ( 2 cos θ , sin θ , 0 ) s p T then we have two eg
dipole
V ( r ) = q 4 π ε 0 r 2 − r 1 r 1 r 2 → 1 4 π ε 0 2 a q cos θ r 2 ( r > > a ) V(r)=\frac{q}{4\pi \varepsilon _0}\frac{r_2-r_1}{r_1r_2}\to \frac{1}{4\pi \varepsilon _0}\frac{2aq\cos \theta}{r^2}(r>>a) V ( r ) = 4 π ε 0 q r 1 r 2 r 2 − r 1 → 4 π ε 0 1 r 2 2 a q cos θ ( r >> a ) then
V ( r , θ ) = 1 4 π ε 0 2 a q cos θ r 2 E r = − ∂ V ∂ r E θ = − ∂ V ∂ θ ⇒ E ⃗ = 2 a q 4 π ε 0 r 3 ( ( 2 cos θ ) r ^ + sin θ θ ^ ) V(r,\theta)=\frac{1}{4\pi \varepsilon _0}\frac{2aq\cos \theta}{r^2}\\E_r=-\frac{\partial V}{\partial r}\\E_\theta=-\frac{\partial V}{\partial \theta}\\\Rightarrow \vec E=\frac{2aq}{4\pi \varepsilon _0 r^3}((2\cos \theta )\hat r+\sin \theta \hat \theta) V ( r , θ ) = 4 π ε 0 1 r 2 2 a q cos θ E r = − ∂ r ∂ V E θ = − ∂ θ ∂ V ⇒ E = 4 π ε 0 r 3 2 a q (( 2 cos θ ) r ^ + sin θ θ ^ )
it’s easy to see that arg max θ ∣ ∣ E ⃗ ∣ ∣ = π 2 \arg \max_{\theta } ||\vec E||=\frac{\pi}{2} arg max θ ∣∣ E ∣∣ = 2 π
eg. disk
d q = 2 π ω ⋅ d ω ⋅ σ d V = d q 4 π ε 0 z 2 + ω 2 = 2 π ω ⋅ d ω ⋅ σ 4 π ε 0 z 2 + ω 2 V = ∫ 0 R 2 π ω ⋅ d ω ⋅ σ 4 π ε 0 z 2 + ω 2 = σ 2 ε 0 ( z 2 + R 2 − z ) E z = − ∂ V ∂ z = − σ 2 ε 0 ( 2 z 2 R 2 + z 2 − 1 ) = σ 2 ε 0 ( 1 − 1 1 + ( R / z ) 2 ) \begin{aligned} &dq=2\pi\omega\cdot d\omega\cdot\sigma \\ &dV=\frac{dq}{4\pi\varepsilon_{0}\sqrt{z^{2}+\omega^{2}}}=\frac{2\pi\omega\cdot d\omega\cdot\sigma}{4\pi\varepsilon_{0}\sqrt{z^{2}+\omega^{2}}} \\ &V=\int_{0}^{R}\frac{2\pi\omega\cdot d\omega\cdot\sigma}{4\pi\varepsilon_{0}\sqrt{z^{2}+\omega^{2}}}=\frac{\sigma}{2\varepsilon_{0}}\big(\sqrt{z^{2}+R^{2}}-z\big) \\ &E_{z}=-\frac{\partial V}{\partial z}=-\frac{\sigma}{2\varepsilon_{0}}(\frac{2z}{2\sqrt{R^{2}+z^{2}}}-1) \\ &=\frac{\sigma}{2\varepsilon_{0}}(1-\frac{1}{\sqrt{1+(R/z)^{2}}}) \end{aligned} d q = 2 πω ⋅ d ω ⋅ σ d V = 4 π ε 0 z 2 + ω 2 d q = 4 π ε 0 z 2 + ω 2 2 πω ⋅ d ω ⋅ σ V = ∫ 0 R 4 π ε 0 z 2 + ω 2 2 πω ⋅ d ω ⋅ σ = 2 ε 0 σ ( z 2 + R 2 − z ) E z = − ∂ z ∂ V = − 2 ε 0 σ ( 2 R 2 + z 2 2 z − 1 ) = 2 ε 0 σ ( 1 − 1 + ( R / z ) 2 1 ) a e.g for getting
v v v with
Δ U \Delta U Δ U 1 2 m v 2 = K = − Δ U = − q Δ V ⇒ v = 2 q Δ V m \frac{1}{2}mv^2=K=-\Delta U=-q\Delta V\Rightarrow v=\sqrt{\frac{2q\Delta V}{m}} 2 1 m v 2 = K = − Δ U = − q Δ V ⇒ v = m 2 q Δ V we can measure α \alpha α
Appendix method of images#
we can see
E ( r ⃗ s ) = σ ( r ⃗ s ) ε 0 E(\vec r_s)=\frac{\sigma(\vec r_s)}{\varepsilon _0} E ( r s ) = ε 0 σ ( r s ) we can see that the induced charge distribution generated with a point of charge and a conductor sheet is the same as which is made by two charges. It can be proved with symmetry theorem.
Chap. 30 Capacitance and Dielectrics# 30-1 Capacitors# Classic Capacitors# Application
flashbulbs s s m s ms m s Laser pulse thermonuclear fusion 1 0 14 W , 1 0 − 9 s , 1 0 8 K 10^{14}W,10^{-9}s,10^8K 1 0 14 W , 1 0 − 9 s , 1 0 8 K Definition of Capacitance : two spatially seperated conductors(+ q / − q +q/-q + q / − q C = q Δ V C=\frac{q}{\Delta V} C = Δ V q
IMPORTANT one single conductor is capacitor!
q = σ A Δ V = − ∫ A B E ⃗ ⋅ d l ⃗ q=\sigma A\\\Delta V=-\int _{A}^B \vec E\cdot \mathrm{d}\vec l q = σ A Δ V = − ∫ A B E ⋅ d l q = σ A Δ V = − ∫ A B E ⃗ ⋅ d l ⃗ q=\sigma A\\\Delta V=-\int _{A}^B \vec E\cdot \mathrm{d}\vec l q = σ A Δ V = − ∫ A B E ⋅ d l since
E A ε 0 = σ A ⇒ E = σ ε 0 ⇒ Δ V = q A ε 0 d ⇒ C = ε 0 A d EA\varepsilon _0= \sigma A\Rightarrow E=\frac{\sigma}{\varepsilon _0}\Rightarrow \Delta V=\frac{q}{A\varepsilon_0}d\Rightarrow C=\frac{\varepsilon _0 A}{d} E A ε 0 = σ A ⇒ E = ε 0 σ ⇒ Δ V = A ε 0 q d ⇒ C = d ε 0 A Application
condenser:C ∝ 1 d → f i x e d Δ V Q ∝ 1 d , I = d Q d t C \propto \frac{1}{d}\xrightarrow{\mathrm{fixed~}\Delta V} Q\propto\frac{1}{d},I=\frac{\mathrm{d} Q}{\mathrm d t} C ∝ d 1 fixed Δ V Q ∝ d 1 , I = d t d Q I I I eg
+ Q , − Q +Q,-Q + Q , − Q Δ V \Delta V Δ V
2 π r ⋅ L ⋅ E ⋅ ε 0 = Q ⇒ E = Q 2 π ε 0 L r 2\pi r \cdot L\cdot E\cdot \varepsilon_0=Q\Rightarrow E=\frac{Q}{2\pi \varepsilon _0 Lr} 2 π r ⋅ L ⋅ E ⋅ ε 0 = Q ⇒ E = 2 π ε 0 L r Q Δ V = ∫ b a E ⃗ ⋅ d l ⃗ = Q 2 π ε L ln b a , C = 2 π ε 0 L ln b a \Delta V=\int_{b}^a \vec E\cdot \mathrm d\vec l =\frac{Q}{2\pi \varepsilon L\ln \frac{b}{a}},C=\frac{2\pi \varepsilon _0 L}{\ln\frac{b}{a}} Δ V = ∫ b a E ⋅ d l = 2 π ε L ln a b Q , C = ln a b 2 π ε 0 L ex
a = r i = 0.15 , b = r o = 2.1 a=r_i=0.15,b=r_o=2.1 a = r i = 0.15 , b = r o = 2.1
C L = 2 π ε 0 ln ( b / a ) = 2 π × 8.85 × 1 0 − 12 ln ( 2.1 / 0.15 ) = 21 × 1 0 − 12 F / m = 21 p F / m \frac{C}{L}=\frac{2\pi\varepsilon_{0}}{\ln(b/a)}=\frac{2\pi\times8.85\times10^{-12}}{\ln(2.1/0.15)}=21\times10^{-12}F / m=21 pF / m L C = ln ( b / a ) 2 π ε 0 = ln ( 2.1/0.15 ) 2 π × 8.85 × 1 0 − 12 = 21 × 1 0 − 12 F / m = 21 pF / m eg
E ⃗ = q r ^ 4 π ε 0 r 2 ⇒ Δ V = q 4 π ε 0 ( 1 a − 1 b ) ⇒ C = 4 π ε 0 a b b − a \vec E=\frac{q\hat r}{4\pi \varepsilon _0 r^2}\Rightarrow \Delta V=\frac{q}{4\pi \varepsilon_0 }\left(\frac{1}{a}-\frac{1}{b}\right)\Rightarrow C=\frac{4\pi \varepsilon _0ab}{b-a} E = 4 π ε 0 r 2 q r ^ ⇒ Δ V = 4 π ε 0 q ( a 1 − b 1 ) ⇒ C = b − a 4 π ε 0 ab for earth R = 6.37 × 1 0 6 m ⇒ C = 7.1 × 1 0 − 4 F = 710 μ F R=6.37\times 10^6 m\Rightarrow C=7.1\times 10^{-4}\mathrm F=710\mu \mathrm F R = 6.37 × 1 0 6 m ⇒ C = 7.1 × 1 0 − 4 F = 710 μ F
Summary# Parallel Plate:C = ε 0 A d C=\frac{\varepsilon _0 A}{d} C = d ε 0 A Cylindrical Capacitor:C = 2 π ε 0 L ln b a C=\frac{2\pi \varepsilon _0 L}{\ln\frac{b}{a}} C = l n a b 2 π ε 0 L Spherical C = 4 π ε 0 a b b − a C=4\pi \varepsilon_0\frac{ab}{b-a} C = 4 π ε 0 b − a ab Parallel & Series#
for capacitors in parallel
V = Q 1 C 1 = Q 2 C 2 ⇒ Q 2 = Q 1 C 2 C 1 C = C 1 + C 2 V=\frac{Q_1}{C_1}=\frac{Q_2}{C_2}\Rightarrow Q_2=Q_1\frac{C_2}{C_1}\\C=C_1+C_2 V = C 1 Q 1 = C 2 Q 2 ⇒ Q 2 = Q 1 C 1 C 2 C = C 1 + C 2 for capacitors in series
V a b = Q C = Q C 1 + Q C 2 ⇒ C = ( 1 C 1 + 1 C 2 ) − 1 V_{ab}=\frac{Q}{C}=\frac{Q}{C_1}+\frac{Q}{C_2}\Rightarrow C=\left(\frac{1}{C_1}+\frac{1}{C_2}\right)^{-1} V ab = C Q = C 1 Q + C 2 Q ⇒ C = ( C 1 1 + C 2 1 ) − 1
1 C = 1 C 3 + 1 C 1 + C 2 \frac{1}{C}=\frac{1}{C_3}+\frac{1}{C_1+C_2} C 1 = C 3 1 + C 1 + C 2 1
C = 2 π ε 0 L ln b a ln d c C=\frac{2\pi \varepsilon _0L}{\ln\frac{b}{a}\ln \frac{d}{c}} C = ln a b ln c d 2 π ε 0 L 30-2 Energy storage in E-field# for paralleled capacitor
d W = V ( q ) d q = q d q C W = ∫ 0 Q q d q C = 1 2 Q 2 C = C V 2 2 ⇒ = 1 2 C V 2 \mathrm d W=V(q)\mathrm d q=\frac{q\mathrm d q}{C}\\ W=\int _{0}^ Q \frac{q\mathrm dq}{C}=\frac{1}{2}\frac{Q^2}{C}=\frac{CV^2}{2}\Rightarrow =\frac{1}{2}CV^2 d W = V ( q ) d q = C q d q W = ∫ 0 Q C q d q = 2 1 C Q 2 = 2 C V 2 ⇒= 2 1 C V 2 in some questions ,we need to verify the fact whether Q Q Q V V V
U = 1 2 Q C 2 = 1 2 Q 2 A ε 0 / d ⇒ E = σ ε 0 = Q ε 0 A ⇒ U = 1 2 E 2 ε 0 A d U=\frac{1}{2}\frac{Q}{C^2}=\frac{1}{2}\frac{Q^2}{A\varepsilon _0/d}\Rightarrow E=\frac{\sigma}{\varepsilon_0}=\frac{Q}{\varepsilon _0 A}\\\Rightarrow U=\frac{1}{2}E^2\varepsilon _0 A d U = 2 1 C 2 Q = 2 1 A ε 0 / d Q 2 ⇒ E = ε 0 σ = ε 0 A Q ⇒ U = 2 1 E 2 ε 0 A d the energy density u = W A d = 1 2 ε 0 E 2 ( J ⋅ m − 3 ) u=\frac{W}{Ad}=\frac{1}{2}\varepsilon _0 E^2(J\cdot m^{-3}) u = A d W = 2 1 ε 0 E 2 ( J ⋅ m − 3 )
you can calculate with u u u
U = ∫ a b 1 2 ε 0 E 2 = ε 0 2 ∫ ( λ 2 π ε 0 r ) 2 L 2 π r d r = 1 2 Q 2 2 π ε 0 L ln b a = 1 2 Q 2 C U=\int_{a}^b \frac{1}{2}\varepsilon _0 E^2=\frac{\varepsilon _0}{2}\int \left(\frac{\lambda }{2\pi \varepsilon _0 r} \right)^2L2\pi r \mathrm d r=\frac{1}{2}\frac{Q^2}{2\pi \varepsilon _0 L}\ln \frac{b}{a}=\frac{1}{2}\frac{Q^2}{C} U = ∫ a b 2 1 ε 0 E 2 = 2 ε 0 ∫ ( 2 π ε 0 r λ ) 2 L 2 π r d r = 2 1 2 π ε 0 L Q 2 ln a b = 2 1 C Q 2 ACT2 cylindrical capacitors
with two cylindrical capacitors (( a , b ) v s ( 2 a , 2 b ) (a,b)~\mathrm{vs}~(2a,2b) ( a , b ) vs ( 2 a , 2 b )
C = 2 π ε o L ln ( r o u t e r r i n n e r ) C=\frac{2\pi\varepsilon_oL}{\ln\left(\frac{r_{outer}}{r_{inner}}\right)} C = ln ( r inn er r o u t er ) 2 π ε o L so C 1 = C 2 C_1=C_2 C 1 = C 2
::: note[P687 30-7]
Problem 30- 7 ( page 687) . \textbf{Problem 30- 7 ( page 687) . } Problem 30- 7 ( page 687) . R R R q = 1.25 n C . ( q=1.25nC.( q = 1.25 n C . ( R ϑ R_{\vartheta} R ϑ
R=6.85cm, q=1.25nC
(a)U=?
(b)u=? (at the surface of the sphere)
(c)R 0 = ? R_0=?~ R 0 = ? R < R 0 , U ′ = 1 2 U R<R_0,U'=\frac{1}{2} U R < R 0 , U ′ = 2 1 U
(a)
C = 4 π ε 0 R U = q 2 2 C = q 2 8 π ε 0 R = 1.03 × 1 0 − 7 J = 103 n J \begin{aligned}&C=4\pi\boldsymbol{\varepsilon}_0R\\&U=\frac{q^2}{2C}=\frac{q^2}{8\pi\boldsymbol{\varepsilon}_0R}=1.03\times10^{-7}J=103nJ\end{aligned} C = 4 π ε 0 R U = 2 C q 2 = 8 π ε 0 R q 2 = 1.03 × 1 0 − 7 J = 103 n J (b)
E = q 4 π ε 0 R 2 u = 1 2 ε 0 E 2 = 1 2 ε 0 q 2 16 π 2 ε 0 2 R 4 = q 2 32 π 2 ε 0 2 R 4 = 25.4 n J / c m 3 \begin{aligned}&E=\frac q{4\pi\varepsilon_0R^2}\\&u=\frac12\varepsilon_0E^2=\frac12\varepsilon_0\frac{q^2}{16\pi^2\varepsilon_0^2R^4}=\frac{q^2}{32\pi^2\varepsilon_0^2R^4}=25.4nJ/cm^3\end{aligned} E = 4 π ε 0 R 2 q u = 2 1 ε 0 E 2 = 2 1 ε 0 16 π 2 ε 0 2 R 4 q 2 = 32 π 2 ε 0 2 R 4 q 2 = 25.4 n J / c m 3 (c)
∫ R R 0 1 2 ε 0 E 2 d ν = ∫ R 0 ∞ 1 2 ε 0 E 2 d ν ∫ R R 0 1 2 ε 0 q 2 16 π 2 ε 0 2 r 4 4 π r 2 d r = ∫ R 0 ∞ 1 2 ε 0 q 2 16 π 2 ε 0 2 r 4 4 π r 2 d r ∫ R R 0 d r r 2 = ∫ R 0 ∞ d r r 2 1 R − 1 R 0 = 1 R 0 R 0 = 2 R = 13.7 c m \begin{aligned} &\int_R^{R_0}\frac12\varepsilon_0E^2d\nu=\int_{R_0}^\infty\frac12\varepsilon_0E^2d\nu \\ &\int_R^{R_0}\frac{1}{2}\varepsilon_0\frac{q^2}{16\pi^2\varepsilon_0^2r^4}4\pi r^2dr=\int_{R_0}^\infty\frac{1}{2}\varepsilon_0\frac{q^2}{16\pi^2\varepsilon_0^2r^4}4\pi r^2dr \\ &\int_R^{R_0}\frac{dr}{r^2}=\int_{R_0}^\infty\frac{dr}{r^2} \\ &\frac1R-\frac1{R_0}=\frac1{R_0} \\ &R_0=2R=13.7cm \end{aligned} ∫ R R 0 2 1 ε 0 E 2 d ν = ∫ R 0 ∞ 2 1 ε 0 E 2 d ν ∫ R R 0 2 1 ε 0 16 π 2 ε 0 2 r 4 q 2 4 π r 2 d r = ∫ R 0 ∞ 2 1 ε 0 16 π 2 ε 0 2 r 4 q 2 4 π r 2 d r ∫ R R 0 r 2 d r = ∫ R 0 ∞ r 2 d r R 1 − R 0 1 = R 0 1 R 0 = 2 R = 13.7 c m 30-3 Dielectrics# Capacitor with dielectrics# definition
Empirical observation : Inserting a non-conducting material between the plates of a capacitor changes the VALUE of the capacitance.dielectric constant C = κ e C 0 C=\kappa _e C_0 C = κ e C 0 κ e > 1 \kappa_e>1 κ e > 1 C 0 C_0 C 0 with dielectric constant κ e \kappa _e κ e Q Q Q
V = Q C = V 0 κ e ⇒ E = E 0 κ e V=\frac{Q}{C}=\frac{V_0}{\kappa_e}\Rightarrow E= \frac{E_0}{\kappa_e} V = C Q = κ e V 0 ⇒ E = κ e E 0 with const V V V
Q ′ = κ e C 0 V Q'=\kappa _e C_0V Q ′ = κ e C 0 V
parallel-plate :C = κ e ε 0 A d C=\frac{\kappa_e \varepsilon _0 A}{d} C = d κ e ε 0 A cylindrical C = κ e 2 π ε 0 L ln b a C=\frac{\kappa_e 2\pi \varepsilon _0 L}{\ln \frac {b}{a}} C = l n a b κ e 2 π ε 0 L spherical C = 4 π ε 0 κ e a b b − a C=4\pi \varepsilon _0\kappa_e\frac{ab}{b-a} C = 4 π ε 0 κ e b − a ab for point charge E = Q 4 π ε 0 κ e r 2 \displaystyle E=\frac{Q}{4\pi \varepsilon _0\kappa_e r^2} E = 4 π ε 0 κ e r 2 Q
C = C 1 C 2 C 1 + C 2 = ε 0 A d 1 + d 2 > ε 0 A d ( d > d 1 + d 2 ) ) C=\frac{C_1C_2}{C_1+C_2}=\frac{\varepsilon _0 A }{d_1+d_2}>\frac{\varepsilon _0 A}{d}(d>d_1+d_2)) C = C 1 + C 2 C 1 C 2 = d 1 + d 2 ε 0 A > d ε 0 A ( d > d 1 + d 2 )) Polarization effect :
V = E d = ( E 0 − E ′ ) d < E 0 d C = q ( E 0 − E ′ ) d > C 0 V=Ed=(E_0-E')d<E_0d\\C=\frac{q}{(E_0-E')d}>C_0 V = E d = ( E 0 − E ′ ) d < E 0 d C = ( E 0 − E ′ ) d q > C 0 microscopic mechanism of polarization# Non-polar dielectrics p ⃗ = q d ⃗ = 0 \vec p=q\vec d=0 p = q d = 0 Polar dielectrics p ⃗ = q d ⃗ ≠ 0 \vec p=q\vec d\neq 0 p = q d = 0 for non-polar dielectrics
we have
Induced electric dipole moment
Electric displacement polarization
Polar dielectrics
∑ p ⃗ ≠ 0 \sum \vec p\neq 0 ∑ p = 0 Alignment polarization
TIP In high frequency field , Electric displacement polarization plays an important role
Polarization# Polarization intensity P ⃗ \vec P P
P ⃗ = ∑ p ⃗ m Δ V ( C ⋅ m − 2 ) = n q l ⃗ \vec P=\cfrac{\sum \vec p_m}{\Delta V} (C\cdot m^{-2})=nq \vec l P = Δ V ∑ p m ( C ⋅ m − 2 ) = n q l
d N = n d V = n l d A cos θ d q ′ = q d N = n q l d A cos θ = P d A cos θ = P ⃗ ∙ d A ⃗ ∮ P ⃗ ∙ d A ⃗ = ∑ o u t q ′ = − ∑ i n q ′ d q ′ = P ⃗ ∙ d A ⃗ = P cos θ ⋅ d A σ ′ = d q ′ d A = P cos θ = P ⃗ ∙ n ⃗ = P n \begin{aligned} &dN=ndV=nldA\cos\theta \\ &dq'=qdN=nqldA\cos\theta \\ &=PdA\cos\theta \\ &=\vec{P}\bullet d\vec{A} \\ &\oint\vec{P}\bullet d\vec{A}=\sum_{out}q'=-\sum_{in}q'\\ &dq'=\vec{P}\bullet d\vec{A}=P\cos\theta\cdot dA\\&\sigma'=\frac{dq'}{dA}=P\cos\theta=\vec{P}\bullet\vec{n}=P_n \end{aligned} d N = n d V = n l d A cos θ d q ′ = q d N = n ql d A cos θ = P d A cos θ = P ∙ d A ∮ P ∙ d A = o u t ∑ q ′ = − in ∑ q ′ d q ′ = P ∙ d A = P cos θ ⋅ d A σ ′ = d A d q ′ = P cos θ = P ∙ n = P n Depolarization Field# E ⃗ = E ⃗ 0 + E ⃗ ′ \vec E=\vec E_0+\vec E' E = E 0 + E ′
σ e ′ = P n = P cos θ d E ′ = d q ′ 4 π ε 0 R 2 = σ e ′ d A 4 π ε 0 R 2 = P cos θ d A 4 π ε 0 R 2 d A = R d θ ⋅ R sin θ d φ = R 2 sin θ d θ d φ d E ′ = P 4 π ε 0 cos θ sin θ d θ d φ d E z ′ = d E ′ cos ( π − θ ) = − d E ′ cos θ = − P 4 π ε 0 cos 2 θ sin θ d θ d φ E z ′ = ∮ z d E z ′ = − P 4 π ε 0 ∫ 0 π cos 2 θ sin θ d θ ∫ 0 2 π d φ = − P 3 ε 0 \begin{aligned} &\sigma_e^{\prime}=P_n=P\cos\theta \\ &dE^{\prime}=\frac{dq^{\prime}}{4\pi\varepsilon_0R^2}=\frac{\sigma_e^{\prime}dA}{4\pi\varepsilon_0R^2}=\frac{P\cos\theta dA}{4\pi\varepsilon_0R^2} \\ &dA=Rd\theta\cdot R\sin\theta d\varphi \\ &=R^{2}\sin\theta d\theta d\varphi \\ &dE'=\frac P{4\pi\varepsilon_0}\cos\theta\sin\theta d\theta d\varphi \\ &dE'_z=dE'\cos(\pi-\theta)=-dE'\cos\theta \\ &=-\frac P{4\pi\varepsilon_0}\cos^2\theta\sin\theta d\theta d\varphi \\ &E_z^{\prime}=\oint_zdE_z^{\prime}=-\frac P{4\pi\varepsilon_0}\int_0^\pi\cos^2\theta\sin\theta d\theta\int_0^{2\pi}d\varphi=-\frac P{3\varepsilon_0} \end{aligned} σ e ′ = P n = P cos θ d E ′ = 4 π ε 0 R 2 d q ′ = 4 π ε 0 R 2 σ e ′ d A = 4 π ε 0 R 2 P cos θ d A d A = R d θ ⋅ R sin θ d φ = R 2 sin θ d θ d φ d E ′ = 4 π ε 0 P cos θ sin θ d θ d φ d E z ′ = d E ′ cos ( π − θ ) = − d E ′ cos θ = − 4 π ε 0 P cos 2 θ sin θ d θ d φ E z ′ = ∮ z d E z ′ = − 4 π ε 0 P ∫ 0 π cos 2 θ sin θ d θ ∫ 0 2 π d φ = − 3 ε 0 P eg2 parallel plate
σ e ′ = P cos θ = P E ′ = σ e ′ ε 0 \sigma_e'=P\cos \theta =P\\ E'=\frac{\sigma_e'}{\varepsilon_0} σ e ′ = P cos θ = P E ′ = ε 0 σ e ′ Polarization law# P ⃗ ⇒ σ e ′ ⇒ E ⃗ ′ ⇒ E ⃗ [ P ⃗ ( E ⃗ ) ] \vec P\Rightarrow \sigma_e'\Rightarrow \vec E'\Rightarrow \vec E[\vec P(\vec E)] P ⇒ σ e ′ ⇒ E ′ ⇒ E [ P ( E )] for general isotropic materials
P ⃗ = χ e ε 0 E ⃗ ( κ e = 1 + χ e ) \vec{P}=\chi_e\varepsilon_0\vec{E}(\kappa _e=1+\chi_e) P = χ e ε 0 E ( κ e = 1 + χ e ) χ e \chi _e χ e
for crystal materials:
( P x P y P z ) = ( χ x x χ x y χ x z χ y x χ y y χ y z χ z x χ z y χ z z ) ( ε 0 E x ε 0 E y ε 0 E z ) \begin{pmatrix}P_x\\P_y\\P_z\end{pmatrix}=\begin{pmatrix}\chi_{xx}\chi_{xy}\chi_{xz}\\\chi_{yx}\chi_{yy}\chi_{yz}\\\chi_{zx}\chi_{zy}\chi_{zz}\end{pmatrix}\begin{pmatrix}\boldsymbol{\varepsilon}_0E_x\\\boldsymbol{\varepsilon}_0E_y\\\boldsymbol{\varepsilon}_0E_z\end{pmatrix} P x P y P z = χ xx χ x y χ x z χ y x χ yy χ yz χ z x χ zy χ zz ε 0 E x ε 0 E y ε 0 E z eg
Electric hysteresis effect Similar to the magnetic hysteresis effect.
Electric Displacement vectorD ⃗ \vec D D # E ⃗ 0 → P ⃗ → σ ′ e → E ′ ⃗ → E ⃗ = E ⃗ 0 + E ′ ⃗ \vec{E}_0\to\vec{P}\to\boldsymbol{\sigma'}_e\to\vec{E'}\to\vec{E}=\vec{E}_0+\vec{E'} E 0 → P → σ ′ e → E ′ → E = E 0 + E ′ D ⃗ \vec D D
Electric displacement vec electric induction
let q 0 q_0 q 0 q ’ q’ q ’
ε 0 ∮ E ⃗ ∙ d A ⃗ = ∑ I n ( q 0 + q ′ ) ∮ P ⃗ ∙ d A ⃗ = − ∑ I n q ′ ∬ ε 0 E ⃗ ∙ d A ⃗ = ∑ I n q 0 − ∮ ∫ P ⃗ ∙ d A ⃗ ∮ ( ε 0 E ⃗ + P ⃗ ) ∙ d A ⃗ = ∑ I n q 0 ∮ D ⃗ ∙ d A ⃗ = ∑ I n D ⃗ = ε 0 E ⃗ + P ⃗ = ( 1 + χ e ) ε 0 E ⃗ = κ e ε 0 E ⃗ ∮ D ⃗ ∙ d A ⃗ = ∑ I n q 0 \begin{aligned} &\varepsilon_0\oint\vec{E}\bullet d\vec{A}=\sum_{In}(q_0+q') \\ &\oint\vec{P}\bullet d\vec{A}=-\sum_{In}q' \\ &\iint\varepsilon_0\vec{E}\bullet d\vec{A}=\sum_{In}q_0-\oint\int\vec{P}\bullet d\vec{A} \\ &\oint(\varepsilon_0\vec{E}+\vec{P})\bullet d\vec{A}=\sum_{In}q_0 \\ &\oint\vec{D}\bullet d\vec{A}=\sum_{In}\\ &\vec D=\varepsilon _0\vec E+\vec P=(1+\chi_e)\varepsilon _0 \vec E=\kappa _e\varepsilon _0 \vec E\\ &\boxed{\oint\vec{D}\bullet d\vec{A}=\sum_{In}q_0} \end{aligned} ε 0 ∮ E ∙ d A = I n ∑ ( q 0 + q ′ ) ∮ P ∙ d A = − I n ∑ q ′ ∬ ε 0 E ∙ d A = I n ∑ q 0 − ∮∫ P ∙ d A ∮ ( ε 0 E + P ) ∙ d A = I n ∑ q 0 ∮ D ∙ d A = I n ∑ D = ε 0 E + P = ( 1 + χ e ) ε 0 E = κ e ε 0 E ∮ D ∙ d A = I n ∑ q 0 eg paralleled plate
∮ D ⃗ ∙ d A = ∑ q 0 D 1 Δ A + D 2 Δ A = σ e 0 Δ A E ⃗ 1 = 0 , D 1 = κ e 1 ε 0 E 1 = 0 , ∴ D 1 = 0 ∴ D = D 2 = σ e 0 = ε 0 E 0 ∴ E = D κ e ε 0 = ε 0 E 0 κ e ε 0 = E 0 κ e D ⃗ = κ e ε 0 E ⃗ \begin{aligned} &\oint\vec{D}\bullet dA=\sum q_0 \\ &D_1\Delta A+D_2\Delta A=\sigma_{e0}\Delta A \\ &\vec{E}_1=0,D_1=\kappa_{e1}\varepsilon_0E_1=0,\therefore D_1=0 \\ &\therefore D=D_2=\sigma_{e0}=\varepsilon_0E_0 \\ &\therefore E=\frac D{\kappa_e\varepsilon_0}=\frac{\varepsilon_0E_0}{\kappa_e\varepsilon_0}=\frac{E_0}{\kappa_e}\\ &\vec D=\kappa _e\varepsilon _0\vec E \end{aligned} ∮ D ∙ d A = ∑ q 0 D 1 Δ A + D 2 Δ A = σ e 0 Δ A E 1 = 0 , D 1 = κ e 1 ε 0 E 1 = 0 , ∴ D 1 = 0 ∴ D = D 2 = σ e 0 = ε 0 E 0 ∴ E = κ e ε 0 D = κ e ε 0 ε 0 E 0 = κ e E 0 D = κ e ε 0 E eg charge in a hole
∮ D ⃗ ∙ d A ⃗ = ∑ q 0 4 π r 2 D = q 0 D = q 0 4 π r 2 E = D κ e ε 0 = q 0 4 π ε 0 κ e r 2 = E 0 κ e \begin{aligned} &\oint\vec{D}\bullet d\vec{A}=\sum q_0 \\ &4\pi r^2D=q_0 \\ &D=\frac{q_0}{4\pi r^2} \\ &E=\frac{D}{\kappa_e\varepsilon_0}=\frac{q_0}{4\pi\varepsilon_0\kappa_er^2}=\frac{E_0}{\kappa_e} \end{aligned} ∮ D ∙ d A = ∑ q 0 4 π r 2 D = q 0 D = 4 π r 2 q 0 E = κ e ε 0 D = 4 π ε 0 κ e r 2 q 0 = κ e E 0 ∮ D ⃗ ⋅ d l ⃗ ≠ 0 \displaystyle \oint \vec D\cdot \mathrm d\vec l\neq 0 ∮ D ⋅ d l = 0
Pressure Electric Effect#
Chap 31 The Steady Current and Conduction Law# 31-1 The Steady Current and Conduction Law# i = lim Δ t → 0 Δ q Δ t = d q d t i=\lim _{\Delta t\to 0}\frac{\Delta q}{\Delta t}=\frac{\mathrm d q}{\mathrm d t} i = Δ t → 0 lim Δ t Δ q = d t d q the current density vector j ⃗ \vec j j
d i = j ⃗ ∙ d A ⃗ , i = ∬ A j ⃗ ∙ d A ⃗ = ∬ A j cos θ d A \begin{aligned}&di=\vec{j}\bullet d\vec{A},\\&i=\iint_A\vec{j}\bullet d\vec{A}\\&=\iint_Aj\cos\theta dA\end{aligned} d i = j ∙ d A , i = ∬ A j ∙ d A = ∬ A j cos θ d A the steady current condition
∬ A j ⃗ ∙ d A ⃗ = 0 ⇔ j 1 Δ A 1 = j 2 Δ A 2 \iint_A\vec{j}\bullet d\vec{A}=0\Leftrightarrow j_1\Delta A_1=j_2\Delta A_2 ∬ A j ∙ d A = 0 ⇔ j 1 Δ A 1 = j 2 Δ A 2 Ohm Law# linear devices :Metal, liquid containing acid, alkali, salt nonlinear devices :Evacuated tube, transistor
Conductance G = 1 R = d I d V ( U n i t : S ) G=\frac{1}{R}=\frac{\mathrm d I}{\mathrm d V}(Unit:S) G = R 1 = d V d I ( U ni t : S ) R = d V d I R=\frac{dV}{dI} R = d I d V R = V I R=\frac{V}{I} R = I V
Resistivity, & conductivity :
we call ρ \rho ρ σ = 1 ρ \sigma =\frac{1}{\rho} σ = ρ 1 R = ρ L A R=\rho \frac{L}{A} R = ρ A L
R = ∫ ρ d l A , σ = 1 ρ R=\int \rho \frac{\mathrm d l}{A}, \sigma =\frac{1}{\rho} R = ∫ ρ A d l , σ = ρ 1 or differential form:j = E ρ = σ E j=\frac{E}{\rho}=\sigma E j = ρ E = σ E
R = ∫ ρ d l A = ∫ a ∞ ρ d r 2 π r 2 = ρ 2 π [ − 1 r ] a ∞ = ρ 2 π a \begin{aligned} &R=\int\rho\frac{dl}{A}=\int_a^\infty\rho\frac{dr}{2\pi r^2} \\ &=\frac{\rho}{2\pi}[-\frac{1}{r}]_a^\infty=\frac{\rho}{2\pi a} \end{aligned} R = ∫ ρ A d l = ∫ a ∞ ρ 2 π r 2 d r = 2 π ρ [ − r 1 ] a ∞ = 2 πa ρ for metal
ρ ( T ) = ρ 0 + α T \rho(T)=\rho_0+\alpha T ρ ( T ) = ρ 0 + α T i = Δ V R i = ∬ j ⃗ ⋅ d A ⃗ ⇒ Δ n V = ∫ E ⃗ ⋅ d l ⃗ R = ∫ ρ d l A i = \frac{\Delta V}{R}\\ i=\iint \vec j \cdot d \vec A\Rightarrow \Delta nV=\int \vec E\cdot d\vec l\\R=\int \rho \frac{dl}{A} i = R Δ V i = ∬ j ⋅ d A ⇒ Δ nV = ∫ E ⋅ d l R = ∫ ρ A d l it;s the integral form of Ohm’s law
and when treating it as differential form
Δ i = Δ V R j Δ A = E Δ l ρ Δ l Δ A j = E ρ = σ E \Delta i =\frac{\Delta V}{R}\\ j\Delta A =\frac{E\Delta l}{\rho \frac{\Delta l}{\Delta A}}\\ j=\frac{E}{\rho}=\sigma E Δ i = R Δ V j Δ A = ρ Δ A Δ l E Δ l j = ρ E = σ E holds for every node
Electric power and Joule Law# different load consumes different energy form
R R R M a c h i n e Machine M a c hin e P = W Δ t = i V = i 2 R = V 2 R P=\frac W{\Delta t}=iV=i^2R=\frac{V^2}R P = Δ t W = iV = i 2 R = R V 2 Unit k W , W kW,W kW , W
1 d e g r e e = 1 k W . h = 3.6 M J 1~degree =1kW.h=3.6MJ 1 d e g ree = 1 kW . h = 3.6 M J
Microscopic explanation of Ohm Law#
drift speed of electric charge
j = 2.4 A / m m 2 b = 8.4 × 1 0 28 m − 3 j = Δ i Δ A = n e u u = j n e = 1.8 × 1 0 − 4 m / s < < v t ≈ 1 0 5 m / s j=2.4A/mm^2\\ b=8.4\times 10^{28}m^{-3}\\ j=\frac{\Delta i}{\Delta A}=neu\\ u=\frac{j}{ne}=1.8\times 10^{-4}m/s<<v_t\approx 10^5m/s j = 2.4 A / m m 2 b = 8.4 × 1 0 28 m − 3 j = Δ A Δ i = n e u u = n e j = 1.8 × 1 0 − 4 m / s << v t ≈ 1 0 5 m / s 31-2 Source and Electromotive Force(emf)# ∮ E ⃗ ∙ d l ⃗ = 0 \oint \vec E\bullet d\vec l =0 ∮ E ∙ d l = 0 only E and no current!
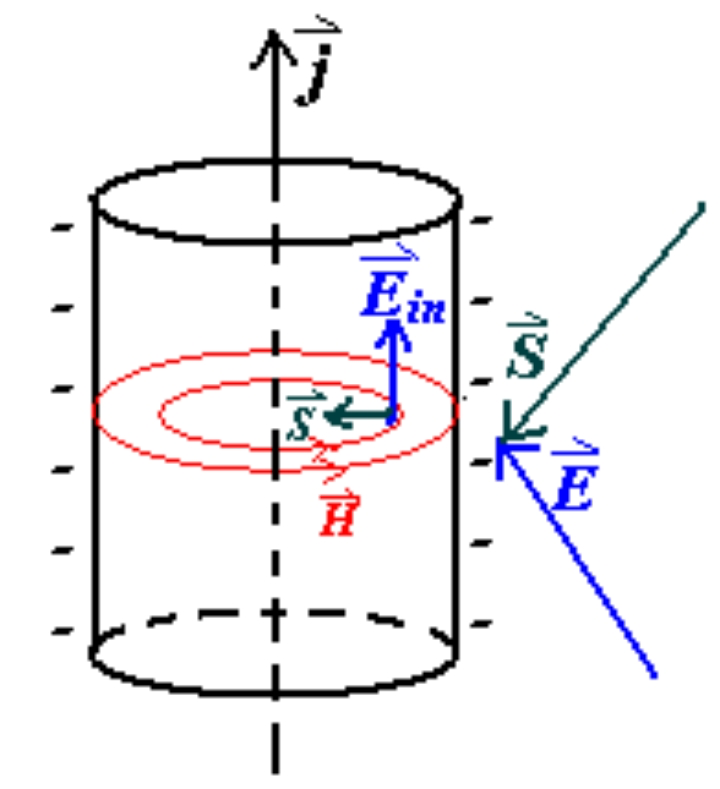
j ⃗ = σ ( K ⃗ + E ⃗ ) \vec j =\sigma(\vec K+\vec E) j = σ ( K + E ) for emf
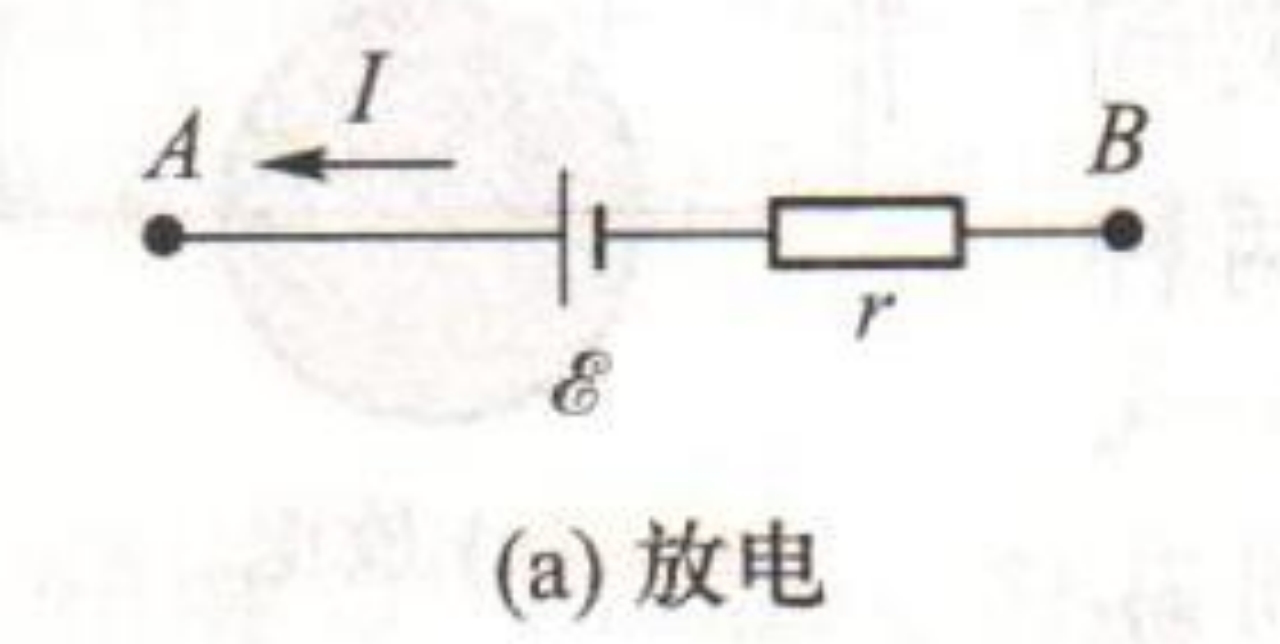
ε = ∮ K ⃗ d l ≈ ∫ − + K ⃗ ⋅ d l ⃗ \varepsilon =\oint \vec K dl\approx \int _{-}^+ \vec K \cdot d\vec l ε = ∮ K d l ≈ ∫ − + K ⋅ d l Terminal Voltage of a Seat# Discharge with R R R ε ′ \varepsilon ' ε ′
Δ V = ∫ + − E ⃗ ⋅ d l ⃗ in a seat : E ⃗ = − K ⃗ + j ⃗ σ Δ V = ∫ − + K ⃗ ⋅ d l ⃗ − ∫ − + ρ j d l cos θ = ε ± ( − j A ∫ − + ρ d l A ) = ε ± i r \Delta V=\int _{+}^{-}\vec E\cdot d\vec l\\ \text{in~a~seat}:\vec E=-\vec K+\frac{\vec j}{\sigma}\\ \Delta V=\int_{-}^+ \vec K\cdot d\vec l-\int_{-}^+ \rho j dl \cos \theta\\=\varepsilon \pm (-jA\int_{-}^+ \frac{\rho d l}{A})=\varepsilon\pm ir Δ V = ∫ + − E ⋅ d l in a seat : E = − K + σ j Δ V = ∫ − + K ⋅ d l − ∫ − + ρ j d l cos θ = ε ± ( − j A ∫ − + A ρ d l ) = ε ± i r the terminal voltage between ends
Discharge:
Δ V A B = ε − i r \Delta V_{AB}=\varepsilon -ir Δ V A B = ε − i r Charge
Δ V A B = ε + i r \Delta V_{AB}=\varepsilon +ir Δ V A B = ε + i r the current and output power for closed circuit# i = ε R + r i=\frac{\varepsilon }{R+r} i = R + r ε P o u t = i V A B = ( ε R + r ) 2 R P_{out}=iV_{AB}=\left(\frac{\varepsilon}{R+r}\right)^2R P o u t = i V A B = ( R + r ε ) 2 R P ˙ o u t = 0 ⇒ ε 2 r − R ( R + r ) 2 = 0 , R ∗ = r \dot P_{out}=0\Rightarrow \varepsilon ^2 \frac{r-R}{(R+r)^2}=0,R^*=r P ˙ o u t = 0 ⇒ ε 2 ( R + r ) 2 r − R = 0 , R ∗ = r
j = σ E ⃗ , S ⃗ = E ⃗ × H ⃗ j=\sigma \vec E,\vec S=\vec E\times \vec H j = σ E , S = E × H 31-3 Simple circuit# Resistors connected in Series and Parallel
R = ∑ R i R=\sum R_i R = ∑ R i R − 1 = ∑ R i − 1 R^{-1}=\sum R_i^{-1} R − 1 = ∑ R i − 1 Voltmeter and Amperemeter
I g = U R g + R m R m = U − I g R g I g = U I g − R g = 199 k Ω I_g =\frac{U}{R_g+R_m}\ R_m=\frac{U-I_gR_g}{I_g}=\frac{U}{I_g}-R_g =199k\Omega I g = R g + R m U R m = I g U − I g R g = I g U − R g = 199 k Ω
I g R g = ( I − I g ) R s R s = I g I − I g R g I_gR_g =(I-I_g)R_s\\R_s=\frac{I_g}{I-I_g}R_g I g R g = ( I − I g ) R s R s = I − I g I g R g