课程相关# 课程信息
名字 :[浙江大学 21120491]高级数据结构与算法分析老师 :卜佳俊其实fds和ads真的可以合成一门课的…
Grading# 成绩组成
HW 10% discussions 10% Research Project + Peer Review 30% 8个项目,每个两组做 MidTerm 10%* (总共60,QA可能有分)
Final Exam 40%(要求大于等于40/100卷面分)
主要分为两个部分:
Project 20 report 6 presentation 10~15min
GD=助教和同学成绩平均值
平衡树专题# BST# IMPORTANT 本题中默认树内不存在相同键值的节点
每个节点至多两个子节点,左子节点的键值小于根节点键值,右子节点的键值大于根节点键值。
对于不同操作的复杂度如下
Insert:O ( h ( T ) ) \mathcal O(h(\mathcal T)) O ( h ( T )) Modify & Find:O ( h ( T ) ) \mathcal O(h(\mathcal T)) O ( h ( T )) Delete:O ( h ( T ) ) \mathcal O(h(\mathcal T)) O ( h ( T )) NOTE 随机情况下,O ( h ( T ) ) = O ( log n ) \mathcal O(h(\mathcal T))=\mathcal O(\log n) O ( h ( T )) = O ( log n )
由琴生不等式
2 E [ x ] ⩽ E [ 2 x ] 2^{\mathbb E[x]}\leqslant \mathbb E[2^x] 2 E [ x ] ⩽ E [ 2 x ] 因此我们可以考虑构造
f x = E [ 2 h x ] f_x=\mathbb E[2^{h_x}]\\ f x = E [ 2 h x ] 考虑用层序遍历对节点重编号,在该意义下,f a i ∈ [ 1 , i ) ( i ⩾ 2 ) fa_i\in [1,i)(i\geqslant 2) f a i ∈ [ 1 , i ) ( i ⩾ 2 )
则
f i = ∑ j = 1 i − 1 f j i − 1 2 = 2 i − 1 ∑ j = 1 i − 1 f j f_{i}=\frac{\displaystyle \sum _{j=1}^{i-1}f_j}{\frac{i-1}{2}}=\frac{2}{i-1}\sum_{j=1}^{i-1}f_j f i = 2 i − 1 j = 1 ∑ i − 1 f j = i − 1 2 j = 1 ∑ i − 1 f j 解递归式得到
S f n = n ( n + 1 ) 2 = O ( n 2 ) Sf_{n}=\frac{n(n+1)}{2}=\mathcal O(n^2) S f n = 2 n ( n + 1 ) = O ( n 2 ) 即
2 E [ h ( T ) ] ⩽ E [ 2 h ( T ) ] ⩽ E [ ∑ x 2 h ( x ) ] = O ( n 2 ) 2^{\mathbb {E}[h(\mathcal T)]}\leqslant \mathbb E[2^{h(\mathcal T)}]\leqslant \mathbb E[\sum _{x} 2^{h(x)}]=\mathcal O(n^2) 2 E [ h ( T )] ⩽ E [ 2 h ( T ) ] ⩽ E [ x ∑ 2 h ( x ) ] = O ( n 2 ) 我们有E [ h ( T ) ] ⩽ O ( log n ) \mathbb E[h(\mathcal T)]\leqslant \mathcal O(\log n) E [ h ( T )] ⩽ O ( log n )
:::
AVL Tree# 我们接下来以AVL Tree为首例引入通过平衡性约束 ,限制和“树高”相关 参量,确保不同操作复杂度。
重要定义
B F ( x ) = h L − h R \mathrm{BF}(x)=h_L-h_R BF ( x ) = h L − h R T \mathcal T T ⇔ \Leftrightarrow ⇔ B F x ∈ { − 1 , 0 , 1 } \mathrm{BF_x}\in \{-1,0,1\} B F x ∈ { − 1 , 0 , 1 } trouble source:(假定当前调整位置为x x x x x x trouble maker:(假定当前调整位置为x x x x x x 点的旋转:指根据点相对其父结点的方向决定旋转方向,具体而言通过将x x x 点的方向:点相对父亲(假设存在)的子边方向 容易发现对于h h h
f h = F h + 3 − 1 = O ( Φ h ) f_h=F_{h+3}-1= \mathcal O(\Phi^h) f h = F h + 3 − 1 = O ( Φ h ) 则有对于n n n O ( log Φ n ) \mathcal O(\log _\Phi n) O ( log Φ n )
增补的操作本质上共两类,单旋和双旋,这里我们采取一个非常简单的口诀
从矛盾点向插入位置走两级同向,转一级分支一次 从矛盾点向插入位置走两级异向,从下往上转两次 Splay Tree# AVL的限制很紧,时刻保证左右子树的高度平衡性,我们考虑将其放松一点,将最坏复杂度变成均摊复杂度。
具体而言给出一个很tricky的方法:每次对一个点进行操作完,就Splay到根。
下面对Splay操作做解释
Splay(x)
是一个递归的过程
x x x x x x x x x x x x x x x x x x 复杂度分析由势能分析给出,这里仅给出构造方案
设Φ ( T ) = ∑ log S x \Phi(\mathcal T)=\sum \log S_x Φ ( T ) = ∑ log S x
其中S x S_x S x x x x
最后可以取 credit c i ˉ = 3 ( R ( x ′ ) − R ( x ) ) + 1 \bar{c_i}=3(R(x')-R(x))+1 c i ˉ = 3 ( R ( x ′ ) − R ( x )) + 1
R-B Tree# 重要定义
接着考虑Insert后染色旋转的操作
分三个阶段考虑
x = f a = u c = R ⇒ x=fa=uc=\mathtt{\color{red} R}\Rightarrow x = f a = u c = R ⇒ x = f a = R , u c = B ⇒ x=fa=\mathtt {\color{red} R},uc=\mathtt {B}\Rightarrow x = f a = R , u c = B ⇒ 首先x , f a x,fa x , f a x , f a x,fa x , f a 对现在的
最后是复杂的Delete操作,这里我们假定已经找到位置并且删除,分类讨论:
(下面内容我故意不放图大家可以自行思考,更能加深体会)
WARNING 下面4种情况比较抽象,要认准一个描述顺序
分类讨论
删x x x 删x x x 删x x x 交换父亲和同侧儿子颜色,转同侧儿子,变为case2 删x x x TIP 一个核心思想是黑节点上移吸收不平衡的部分
B+ Tree# B+ Tree是一种扁平化索引结构,其在连续地址优势下相对红黑树更为高效(内存,外存)
这里我们按照2 , 3 , 4 2,3,4 2 , 3 , 4
每个非节点储存至多3 3 3 4 4 4
需要考虑的是插入问题,在发生溢出现象时,我们需要进行分裂操作,具体而言我们采取二分策略。假设出现根的分裂情况则向上新开一层。
NOTE 红黑树和标准的 B+树存在同构关系
*Treap# Inverted File Index# 在没有pagerank理论前,我们考虑使用preindex技术,定期建立 term-document incidence matrix——信息关联矩阵。采取压缩计数,对每个词建立元组vector序列,信息查找过程可以转化为集合求交过程
具体而言,反转文件索引分为下面几个步骤
word stemming stop filter access termsearch tree hash 有序性 vs 低复杂度 Deal with sparling mem 数据量大后,我们考虑改善index范式
distributed index
Term-partitional index Document-partitional index Dynamic indexing
Compression,对位置序列做差分
Threshold: 回答排序
评估层面上,information retrievals
Precision: 接收到的里面相关的占比 Recall: 相关的接收到的占比 现代索引优化技术
Page rank BERT Semantic Web RankBrain Latent Semantic Indexing (LSI) TF-IDF 堆专题# IMPORTANT 下面的堆均指小根堆,不加修饰词时,所有关于堆的描述均指向二叉堆
操作 \ 数据结构1 配对堆 二叉堆 左偏树 二项堆 斐波那契堆 插入(insert) O ( 1 ) O(1) O ( 1 ) O ( log n ) O(\log n) O ( log n ) O ( log n ) O(\log n) O ( log n ) O ( log n ) O(\log n) O ( log n ) 2 O ( 1 ) O(1) O ( 1 ) 查询最小值(find-min) O ( 1 ) O(1) O ( 1 ) O ( 1 ) O(1) O ( 1 ) O ( 1 ) O(1) O ( 1 ) O ( 1 ) O(1) O ( 1 ) 3 O ( 1 ) O(1) O ( 1 ) 删除最小值(delete-min) O ( log n ) O(\log n) O ( log n ) 3 O ( log n ) O(\log n) O ( log n ) O ( log n ) O(\log n) O ( log n ) O ( log n ) O(\log n) O ( log n ) O ( log n ) O(\log n) O ( log n ) 3 合并 (merge) O ( 1 ) O(1) O ( 1 ) O ( n ) O(n) O ( n ) O ( log n ) O(\log n) O ( log n ) O ( log n ) O(\log n) O ( log n ) O ( 1 ) O(1) O ( 1 ) 减小一个元素的值 (decrease-key) o ( log n ) o(\log n) o ( log n ) Ω ( log log n ) \Omega(\log \log n) Ω ( log log n ) O ( 2 2 log log n ) O(2^{2\sqrt{\log \log n}}) O ( 2 2 l o g l o g n ) 3 O ( log n ) O(\log n) O ( log n ) O ( log n ) O(\log n) O ( log n ) O ( log n ) O(\log n) O ( log n ) O ( 1 ) O(1) O ( 1 ) 3 是否支持可持久化 × \times × ✓ \checkmark ✓ ✓ \checkmark ✓ ✓ \checkmark ✓ × \times ×
a.m表示均摊
Binary Heaps# 我们从最基础的二叉堆开始复习
二叉堆采取堆式编号,数组,含有
Find_minpercolate uppercolate down三种操作
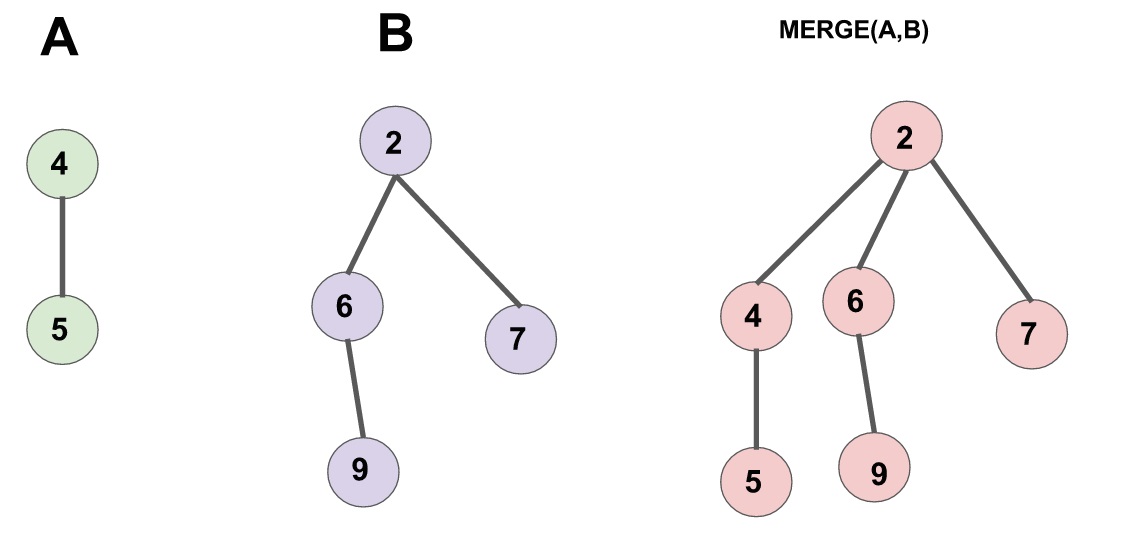
实现略去,这里需要记忆的是关于堆的合并,其本质是重建
Leftist Heaps# 重要定义
NPL: 空路径距离,到最近的没有两个子节点的子树内节点的距离 左偏树要求:∀ x ∈ H , N P L ( L ) ⩾ N P L ( R ) \forall x\in\mathcal H,NPL(L)\geqslant NPL(R) ∀ x ∈ H , NP L ( L ) ⩾ NP L ( R ) 基于定义,我们有
N P L ( x ) = N P L ( R ) + 1 NPL(x)=NPL(R)+1 NP L ( x ) = NP L ( R ) + 1 x x x r r r 2 r − 1 2^r-1 2 r − 1 换一句话,n n n O ( log n ) \mathcal O(\log n) O ( log n )
我们依赖这个设计合并
先比较当前两个待合并子树的根结点的键值,选择较小(较大)的那个作为根结点,其左子树依然为左子树,右子树和另一个合并子树合并,递归
更新完后,检查左偏性质并交换
这里容易发现递归层数为两棵子树的右路径长和,因此单次合并复杂度为O ( log n ) \mathcal O(\log n) O ( log n )
Skew Heaps# CAUTION 这里提到的斜堆的合并定义为,在一边为空时必须对非空的一侧的右路径进行交换,ADS考试中采取的是这种定义而非标准定义 ,两者复杂性是等价的,但是证明方式构造不同。
重要定义
heavy/light node:S R ⩾ 1 2 S x S_R\geqslant \frac{1}{2}S_x S R ⩾ 2 1 S x 我们丢弃NPL,正如AVL舍弃平衡性判定
具体而言,我们总是在合并两棵子树后交换新根的两个子树
合理性上的话,我们总是往原来右侧的路径上合并 ,交换能够有效平衡累积
下面考虑势能分析给出均摊分析
在给出构造前,我们先考虑定性刻画合并的结果
:::
每棵树到全局最大值前的路径全会交换
依赖这个,我们能给出斜堆合并结果的迭代性质刻画
合并后堆的右路径为两个堆右路径的排序 所有左子树为原有左子树 最后右路径上左右子树交换 复杂度分析
heavy node一旦发生合并反转一定变成light node
Light node发生合并反转可以变成heavy node
假设两者互换,则一定在原先的右路径(只有右路径上的点的才会发生子树改变)
设l 1 , l 2 , h 1 , h 2 l_1,l_2,h_1,h_2 l 1 , l 2 , h 1 , h 2
我们思考的起点是
c i ⩽ l 1 + h 1 + l 2 + h 2 c_i\leqslant l_1+h_1+l_2+h_2 c i ⩽ l 1 + h 1 + l 2 + h 2 依赖定义,对于重节点总数的改变Δ Φ ⩽ l 1 + l 2 − h 1 − h 2 \Delta \Phi \leqslant l_1+l_2-h_1-h_2 ΔΦ ⩽ l 1 + l 2 − h 1 − h 2 定义势能函数
Φ ( H ) = ∑ x ∈ H [ S R ⩾ 1 2 S x ] \Phi(\mathcal H)=\sum _{x\in \mathcal H}[S_R\geqslant \frac{1}{2}S_x] Φ ( H ) = x ∈ H ∑ [ S R ⩾ 2 1 S x ] credit
c ^ i = c i + Φ ( H ′ ) − Φ ( H 1 ) − Φ ( H 2 ) = c i + Δ Φ \hat c_i=c_i+\Phi(\mathcal H')-\Phi(\mathcal H_1)-\Phi(\mathcal H_2)=c_i+\Delta \Phi c ^ i = c i + Φ ( H ′ ) − Φ ( H 1 ) − Φ ( H 2 ) = c i + ΔΦ 我们可以得到
c ^ i ⩽ 2 ( l 1 + l 2 ) \hat c_i\leqslant 2(l_1+l_2) c ^ i ⩽ 2 ( l 1 + l 2 ) 我们证明l i = O ( log n ) l_i=\mathcal O(\log n) l i = O ( log n )
显然c ^ i = O ( log n ) \hat c_i=\mathcal O(\log n) c ^ i = O ( log n )
Binomial heap/queue# 这里我们开始思考 堆-优先队列 的意义,堆从目的上和搜索树有本质差异,其核心维护优先级的特性可以实现
我们讨论树型结构的堆,森林结构的堆,锻炼摊还分析
补充定义
二项树是一个递归定义的树序列B 0 B_0 B 0 B i B_i B i B i − 1 B_{i-1} B i − 1 B i − 1 B_{i-1} B i − 1 B k B_k B k d d d ( k d ) \binom{k}{d} ( d k ) N N N d 1 , d 2 ⋯ , d π N : N = ∑ i = 1 π N 2 i d_1,d_2\cdots,d_{\pi_N}:N=\sum _{i=1}^{\pi_N}2^i d 1 , d 2 ⋯ , d π N : N = ∑ i = 1 π N 2 i 给出合并操作
下面我们用C 11 = 1011 C_{11}=\mathtt{1011} C 11 = 1011 { B 3 , B 1 , B 0 } \{B_3,B_1,B_0\} { B 3 , B 1 , B 0 }
那么我们对两个二项队列的合并过程本质上是在做二进制加法
换一句话,我们实际上只解决相等大小的二项树
即合并操作可以被形式化表示成M e r g e k ∈ Σ ( B k 1 , B k 2 ) \mathrm{Merge}_{k\in \Sigma}(B_{k1},B_{k2}) Merge k ∈ Σ ( B k 1 , B k 2 )
由于∣ Σ ∣ = O ( log n ) |\Sigma|=\mathcal O(\log n) ∣Σ∣ = O ( log n )
删除操作/弹堆首是朴素的,你找到出现问题的堆拆开,在按序合并即可
显然复杂度是O ( log n ) \mathcal O(\log n) O ( log n )
显然我们可以说明Insert的单次复杂度是O ( log n ) \mathcal O(\log n) O ( log n ) O ( 1 ) \mathcal O(1) O ( 1 )
proof 1 聚合分析
容易发现每次合并的具体贡献是可以算出来的
具体而言
c i = p o p _ c o u n t ( i ⊕ i − 1 ) − 1 c_i=\mathrm{pop\_count}(i\oplus i-1)-1 c i = pop_count ( i ⊕ i − 1 ) − 1
则
∑ i = 1 n c i ⩽ ∑ i = 1 n p o p _ c o u n t ( i ⊕ i − 1 ) − 1 ⩽ ∑ i = 1 n s u f f i x ( i ) + 1 ( 2 k > n ) ⩽ n + ∑ i = 1 2 k − 1 s u f f i x ( i ) ⩽ n + ∑ i = 1 k i 2 ( k − i ) ⩽ n + 2 k ∑ i = 1 k i 2 i ⩽ n + 2 k ⩽ 3 n \sum _{i=1}^n c_i\leqslant \sum _{i=1}^n\mathrm{pop\_count}(i\oplus i-1)-1\leqslant \sum_{i=1}^{n} \mathrm{suffix(i)+1}\\(2^k>n)\leqslant n+\sum _{i=1}^{2^k-1}\mathrm{suffix(i)}\\\leqslant n+ \sum _{i=1}^k i 2^{(k-i)}\leqslant n+2^k\sum _{i=1}^k\frac{i}{2^{i}}\leqslant n+2^k\leqslant 3n i = 1 ∑ n c i ⩽ i = 1 ∑ n pop_count ( i ⊕ i − 1 ) − 1 ⩽ i = 1 ∑ n suffix ( i ) + 1 ( 2 k > n ) ⩽ n + i = 1 ∑ 2 k − 1 suffix ( i ) ⩽ n + i = 1 ∑ k i 2 ( k − i ) ⩽ n + 2 k i = 1 ∑ k 2 i i ⩽ n + 2 k ⩽ 3 n 当然上述放缩并没有意义,这里纯属习惯动作
后面的不等式可以参考建堆
proof 2 势能分析
c i = p o p _ c o u n t ( i ⊕ i − 1 ) − 1 c_i=\mathrm{pop\_count}(i\oplus i-1)-1 c i = pop_count ( i ⊕ i − 1 ) − 1 定义Φ ( i ) = p o p _ c o u n t ( i ) \Phi(i)=\mathrm{pop\_count(i)} Φ ( i ) = pop_count ( i )
则c ^ i = c i + Φ ( i ) − Φ ( i − 1 ) = 2 \hat c_i=c_{i}+\Phi(i)-\Phi(i-1)=2 c ^ i = c i + Φ ( i ) − Φ ( i − 1 ) = 2
后面没必要说了
这里也可以由Δ Φ ( i ) \Delta\Phi(i) ΔΦ ( i )
::: tip[proof 3 账分析]
这个反而更加有点tricky
你考虑成每个人给两块钱,出现就扣钱,合并确保根能给你就行
:::
复杂度分析上,有一个有争议的,Find_min到底当成O ( 1 ) \mathcal O(1) O ( 1 ) O ( log n ) \mathcal O(\log n) O ( log n )
Fibonacci heap# IMPORTANT 本节内容参考自《Introduction to Algorithms(Third Edition)》Chap19
可合并堆的性质重申
操作(最坏情形)(摊近) 二项堆 斐波那契堆 MAKE-HEAP Θ ( 1 ) Θ ( 1 ) INSERT Θ ( lg n ) Θ ( 1 ) MNMUM Θ ( 1 ) Θ ( 1 ) EXTRACT-MIN Θ ( lg n ) O ( lg n ) UNION Θ ( n ) Θ ( 1 ) DECREASE-KEY Θ ( lg n ) Θ ( 1 ) DELETE Θ ( lg n ) O ( lg n ) \begin{array}{|ccc|}\hline\text{操作(最坏情形)(摊近)}&\text{二项堆}&\text{斐波那契堆}\\\hline\text{MAKE-HEAP}&\Theta(1)&\Theta(1)\\\text{INSERT}&\Theta(\lg n)&\Theta(1)\\\text{MNMUM}&\Theta(1)&\Theta(1)\\\text{EXTRACT-MIN}&\Theta(\lg n)&O(\lg n)\\\text{UNION}&\Theta(n)&\Theta(1)\\\text{DECREASE-KEY}&\Theta(\lg n)&\Theta(1)\\\text{DELETE}&\Theta(\lg n)&O(\lg n)\\\hline\end{array} 操作 ( 最坏情形 )( 摊近 ) MAKE-HEAP INSERT MNMUM EXTRACT-MIN UNION DECREASE-KEY DELETE 二项堆 Θ ( 1 ) Θ ( lg n ) Θ ( 1 ) Θ ( lg n ) Θ ( n ) Θ ( lg n ) Θ ( lg n ) 斐波那契堆 Θ ( 1 ) Θ ( 1 ) Θ ( 1 ) O ( lg n ) Θ ( 1 ) Θ ( 1 ) O ( lg n ) 容易发现二项堆在UNION或者说Merge上表现很差,我们基于这些问题给出一个更优秀的队列实现——斐波纳契堆/队列
定义
斐波纳契堆是一个最小堆序的有根多叉树集合根被环形双向链表串起来 每个点具有 child,left,right,parent,degree,mark属性,表示孩子列表,左右兄弟和父节点以及度数; 注意根与根(root list),儿子与儿子,兄弟与兄弟,child list的指向是随机的 x . m a r k x.mark x . ma r k x x x 在成为别人的孩子后 ,是否失去国孩子,新产生时为0,成为另一个节点孩子后清零。我们通过H . m i n H.min H . min H . n H.n H . n 斐波纳契对用到的势函数Φ ( H ) = t ( H ) + 2 m ( H ) \Phi(\mathcal H)=t(\mathcal H)+2m(\mathcal H) Φ ( H ) = t ( H ) + 2 m ( H ) t ( H ) t(\mathcal H) t ( H ) m ( H ) m(\mathcal H) m ( H ) 下面我们对于每个操作按照实现规范->势能变化的顺序介绍
Init# H . n = 0 , H . m i n = N I L , Φ ( H ) = 0 H.n=0,H.min=\mathrm{NIL},\Phi(\mathcal H)=0 H . n = 0 , H . min = NIL , Φ ( H ) = 0
摊还代价就是实际代价 O ( 1 ) \mathcal O(1) O ( 1 )
Insert# 直接生成全空的单节点插到根列表中,然后更新最小堆
F I B _ H E A P _ I N S E R T ( H , x ) 1. x . degree = 0 2. x . p = N I L 3. x . child = N I L 4. x . mark = F A L S E 5. if H . min = = N I L 6. create a root list for H containing just x 7. H . min = x 8. else insert x into H ’s root list 9. if x . key < H . min . key 10. H . min = x 11. H . n = H . n + 1 \begin{aligned} &\mathrm{FIB\_HEAP\_INSERT}(H, x) \\ 1.\ & x.\text{degree} = 0 \\ 2.\ & x.\text{p} = \mathrm{NIL} \\ 3.\ & x.\text{child} = \mathrm{NIL} \\ 4.\ & x.\text{mark} = \mathrm{FALSE} \\ 5.\ & \text{if } H.\text{min} == \mathrm{NIL} \\ 6.\ & \quad \text{create a root list for } H \text{ containing just } x \\ 7.\ & \quad H.\text{min} = x \\ 8.\ & \text{else insert } x \text{ into } H\text{'s root list} \\ 9.\ & \quad \text{if } x.\text{key} < H.\text{min}.\text{key} \\ 10.\ & \quad \quad H.\text{min} = x \\ 11.\ & H.\text{n} = H.\text{n} + 1 \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. FIB_HEAP_INSERT ( H , x ) x . degree = 0 x . p = NIL x . child = NIL x . mark = FALSE if H . min == NIL create a root list for H containing just x H . min = x else insert x into H ’s root list if x . key < H . min . key H . min = x H . n = H . n + 1 Δ Φ = ( ( t ( H ) + 1 ) + 2 m ( H ) ) − ( ( t ( H ) ) + 2 m ( H ) ) = 1 \Delta \Phi=((t(\mathcal H)+1)+2m(\mathcal H))-((t(\mathcal H))+2m(\mathcal H))=1 ΔΦ = (( t ( H ) + 1 ) + 2 m ( H )) − (( t ( H )) + 2 m ( H )) = 1 c ^ = O ( 1 ) + 1 = O ( 1 ) \hat c=\mathcal O(1)+1=\mathcal O(1) c ^ = O ( 1 ) + 1 = O ( 1 )
Findmin# O ( 1 ) \mathcal O(1) O ( 1 )
Merge/UNION# 简单的链接根链表,去诶的那个新的最小节点
F I B _ H E A P _ U N I O N ( H 1 , H 2 ) 1. H = MAKE-FIB-HEAP() 2. H . min = H 1 . min 3. concatenate the root list of H 2 with the root list of H 4. if ( H 1 . min = NIL ) or ( H 2 . min ≠ NIL and H 2 . min . key < H 1 . min . key ) 5. H . min = H 2 . min 6. H . n = H 1 . n + H 2 . n 7. return H \begin{aligned} &\mathbf{FIB\_HEAP\_UNION}(H_1, H_2) \\ 1.\ & H = \text{MAKE-FIB-HEAP()} \\ 2.\ & H.\text{min} = H_1.\text{min} \\ 3.\ & \text{concatenate the root list of } H_2 \\&\text{ with the root list of } H \\ 4.\ & \text{if } (H_1.\text{min} = \text{NIL}) \text{ or } \\&(H_2.\text{min} \neq \text{NIL} \text{ and } H_2.\text{min}.\text{key} < H_1.\text{min}.\text{key}) \\ 5.\ & \quad H.\text{min} = H_2.\text{min} \\ 6.\ & H.\text{n} = H_1.\text{n} + H_2.\text{n} \\ 7.\ & \text{return } H \end{aligned} 1. 2. 3. 4. 5. 6. 7. FIB_HEAP_UNION ( H 1 , H 2 ) H = MAKE-FIB-HEAP() H . min = H 1 . min concatenate the root list of H 2 with the root list of H if ( H 1 . min = NIL ) or ( H 2 . min = NIL and H 2 . min . key < H 1 . min . key ) H . min = H 2 . min H . n = H 1 . n + H 2 . n return H Δ Φ = 0 ⇒ c ^ = O ( 1 ) \Delta \Phi=0\Rightarrow \hat c=\mathcal O(1) ΔΦ = 0 ⇒ c ^ = O ( 1 ) F I B _ H E A P _ E X T R A C T _ M I N ( H ) 1. z = H . min 2. if z ≠ NIL 3. for each child x of z 4. add x to the root list of H 5. x . p = NIL 6. remove z from the root list of H 7. if z = z . right 8. H . min = NIL 9. else H . min = z . right 10. CONSOLIDATE ( H ) 11. H . n = H . n − 1 12. return z \begin{aligned} &\mathbf{FIB\_HEAP\_EXTRACT\_MIN}(H) \\ 1.\ & z = H.\text{min} \\ 2.\ & \text{if } z \neq \text{NIL} \\ 3.\ & \quad \text{for each child } x \text{ of } z \\ 4.\ & \quad \quad \text{add } x \text{ to the root list of } H \\ 5.\ & \quad \quad x.\text{p} = \text{NIL} \\ 6.\ & \quad \text{remove } z \text{ from the root list of } H \\ 7.\ & \quad \text{if } z = z.\text{right} \\ 8.\ & \quad \quad H.\text{min} = \text{NIL} \\ 9.\ & \quad \text{else } H.\text{min} = z.\text{right} \\ 10.\ & \quad\quad\text{CONSOLIDATE}(H) \\ 11.\ & \quad H.\text{n} = H.\text{n} - 1 \\ 12.\ & \text{return } z \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. FIB_HEAP_EXTRACT_MIN ( H ) z = H . min if z = NIL for each child x of z add x to the root list of H x . p = NIL remove z from the root list of H if z = z . right H . min = NIL else H . min = z . right CONSOLIDATE ( H ) H . n = H . n − 1 return z 首先把最小根的孩子全部挂上去,然后我们现在随便把H.min指向原来的根 ,进入CONSOLIDATE 过程
CONSOLIDATING 合并# 一言一蔽之
找到相同度数的x , y x,y x , y y y y x x x y y y A A A
具体实现上,我们先找一个根x = w x=w x = w d d d A [ d ] = y A[d]=y A [ d ] = y x ′ ← ( y → x ) x'\leftarrow (y\to x) x ′ ← ( y → x )
处理完之后,我们可以基于A来更新H \mathcal H H
C O N S O L I D A T E ( H ) 1. let A [ 0 … D ( H . n ) ] be a new array 2. for i = 0 to D ( H . n ) 3. A [ i ] = N I L 4. for each node w in the root list of H 5. x = w 6. d = x . degree 7. while A [ d ] ≠ N I L 8. y = A [ d ] / another node with the same degree as x 9. i f x . key > y . key 10. exchange x with y 11. FIB-HEAP-LINK ( H , y , x ) 12. A [ d ] = N I L 13. d = d + 1 14. A [ d ] = x 15. H . min = N I L 16. for i = 0 to D ( H . n ) 17. i f A [ i ] ≠ N I L 18. i f H . min = N I L 19. create a root list for H containing just A [ i ] 20. H . min = A [ i ] 21. e l s e insert A [ i ] into H ’s root list 22. i f A [ i ] . key < H . min . key 23. H . min = A [ i ] \begin{aligned} &\mathbf{CONSOLIDATE}(H) \\ 1.\ & \text{let } A[0 \dots D(H.\text{n})] \text{ be a new array} \\ 2.\ & \text{for } i = 0 \text{ to } D(H.\text{n}) \\ 3.\ & \quad A[i] = \mathbf{NIL} \\ 4.\ & \text{for each node } w \text{ in the root list of } H \\ 5.\ & \quad x = w \\ 6.\ & \quad d = x.\text{degree} \\ 7.\ & \quad \text{while } A[d] \neq \mathbf{NIL} \\ 8.\ & \quad \quad y = A[d] \quad / \text{another node with the same degree as } x \\ 9.\ & \quad \quad \mathbf{if } x.\text{key} > y.\text{key} \\ 10.\ & \quad \quad \quad \text{exchange } x \text{ with } y \\ 11.\ & \quad \quad \text{FIB-HEAP-LINK}(H, y, x) \\ 12.\ & \quad \quad A[d] = \mathbf{NIL} \\ 13.\ & \quad \quad d = d + 1 \\ 14.\ & \quad A[d] = x \\ 15.\ & H.\text{min} = \mathbf{NIL} \\ 16.\ & \text{for } i = 0 \text{ to } D(H.\text{n}) \\ 17.\ & \quad \mathbf{if } A[i] \neq \mathbf{NIL} \\ 18.\ & \quad \quad \mathbf{if } H.\text{min} = \mathbf{NIL} \\ 19.\ & \quad \quad \quad \text{create a root list for } H \text{ containing just } A[i] \\ 20.\ & \quad \quad \quad H.\text{min} = A[i] \\ 21.\ & \quad \mathbf{else } \text{insert } A[i] \text{ into } H\text{'s root list} \\ 22.\ & \quad \mathbf{if } A[i].\text{key} < H.\text{min}.\text{key} \\ 23.\ & \quad \quad H.\text{min} = A[i] \\ \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. CONSOLIDATE ( H ) let A [ 0 … D ( H . n )] be a new array for i = 0 to D ( H . n ) A [ i ] = NIL for each node w in the root list of H x = w d = x . degree while A [ d ] = NIL y = A [ d ] / another node with the same degree as x if x . key > y . key exchange x with y FIB-HEAP-LINK ( H , y , x ) A [ d ] = NIL d = d + 1 A [ d ] = x H . min = NIL for i = 0 to D ( H . n ) if A [ i ] = NIL if H . min = NIL create a root list for H containing just A [ i ] H . min = A [ i ] else insert A [ i ] into H ’s root list if A [ i ] . key < H . min . key H . min = A [ i ] 用到的连接过程
FIB-HEAP-LINK ( H , y , x ) 1. remove y from the root list of H 2. make y a child of x , incrementing x . degree 3. y . mark = FALSE \begin{aligned} &\text{FIB-HEAP-LINK}(H, y, x) \\ 1.\ & \text{remove } y \text{ from the root list of } H \\ 2.\ & \text{make } y \text{ a child of } x, \text{ incrementing } x.\text{degree} \\ 3.\ & y.\text{mark} = \text{FALSE} \end{aligned} 1. 2. 3. FIB-HEAP-LINK ( H , y , x ) remove y from the root list of H make y a child of x , incrementing x . degree y . mark = FALSE 这一部分的复杂度分析最为复杂,首先引入引理
Lemma 1: sup of max_degree
设D ( n ) D(n) D ( n ) n n n
则D ( n ) = O ( ln n ) D(n)=\mathcal O(\ln n) D ( n ) = O ( ln n )
现在返回来考虑摊还代价,注意这里没有点被标记
Δ Φ ⩽ ( ( D ( n ) + 1 ) + 2 m ( H ) ) − ( t ( H ) + 2 m ( H ) ) c i = O ( D ( n ) + t ( H ) ) \Delta \Phi \leqslant ((D(n)+1)+2m(\mathcal H))-(t(\mathcal H)+2m(\mathcal H))\\ c_i=\mathcal O(D(n)+t(\mathcal H)) ΔΦ ⩽ (( D ( n ) + 1 ) + 2 m ( H )) − ( t ( H ) + 2 m ( H )) c i = O ( D ( n ) + t ( H )) 这里解释一下基础操作数
循环本身一定不会多于最终分裂出来的根数
c ^ i = O ( D ( n ) ) = O ( log n ) \hat c_i=\mathcal O(D(n))=\mathcal O(\log n) c ^ i = O ( D ( n )) = O ( log n )
DECREASE-KEY# 简单来说,我们将节点剪切,并考虑级联切断 过程
补充定义
F I B _ H E A P _ D E C R E A S E _ K E Y ( H , x , k ) 1. if k > x . key 2. error: "new key is greater than current key" 3. x . key = k 4. y = x . p 5. i f y ≠ NIL and x . key < y . key 6. C U T ( H , x , y ) 7. C A S C A D I N G _ C U T ( H , y ) 8. i f x . key < H . min . key 9. H . min = x \begin{aligned} &\mathbf{FIB\_HEAP\_DECREASE\_KEY}(H, x, k) \\ 1.\ & \text{if } k > x.\text{key} \\ 2.\ & \quad \text{error: "new key is greater than current key"} \\ 3.\ & x.\text{key} = k \\ 4.\ & y = x.\text{p} \\ 5.\ & \mathbf{if } y \neq \text{NIL} \text{ and } x.\text{key} < y.\text{key} \\ 6.\ & \quad \mathsf{CUT}(H, x, y) \\ 7.\ & \quad \mathsf{CASCADING\_CUT}(H, y) \\ 8.\ & \mathbf{if } x.\text{key} < H.\text{min}.\text{key} \\ 9.\ & \quad H.\text{min} = x \\ \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. FIB_HEAP_DECREASE_KEY ( H , x , k ) if k > x . key error: "new key is greater than current key" x . key = k y = x . p if y = NIL and x . key < y . key CUT ( H , x , y ) CASCADING_CUT ( H , y ) if x . key < H . min . key H . min = x C U T ( H , x , y ) 1. remove x from the child list of y , decrementing y . degree 2. add x to the root list of H 3. x . p = NIL 4. x . mark = FALSE \begin{aligned} &\mathbf{CUT}(H, x, y) \\ 1.\ & \text{remove } x \text{ from the child list of } y, \text{ decrementing } y.\text{degree} \\ 2.\ & \text{add } x \text{ to the root list of } H \\ 3.\ & x.\text{p} = \text{NIL} \\ 4.\ & x.\text{mark} = \text{FALSE} \\ \end{aligned} 1. 2. 3. 4. CUT ( H , x , y ) remove x from the child list of y , decrementing y . degree add x to the root list of H x . p = NIL x . mark = FALSE C A S C A D I N G _ C U T ( H , y ) 1. z = y . p 2. i f z ≠ NIL 3. i f y . mark = F A L S E 4. y . mark = T R U E 5. e l s e C U T ( H , y , z ) 6. C A S C A D I N G _ C U T ( H , z ) \begin{aligned} &\mathsf{CASCADING\_CUT}(H, y) \\ 1.\ & z = y.\text{p} \\ 2.\ & \mathbf{if } z \neq \text{NIL} \\ 3.\ & \quad \mathbf{if } y.\text{mark} = \mathbf{FALSE} \\ 4.\ & \quad \quad y.\text{mark} = \mathbf{TRUE} \\ 5.\ & \quad \mathbf{else} \ \mathsf{CUT}(H, y, z) \\ 6.\ & \quad \mathsf{CASCADING\_CUT}(H, z) \\ \end{aligned} 1. 2. 3. 4. 5. 6. CASCADING_CUT ( H , y ) z = y . p if z = NIL if y . mark = FALSE y . mark = TRUE else CUT ( H , y , z ) CASCADING_CUT ( H , z ) 这里我们假设级连切除的次数是c c c
Δ Φ ⩽ ( ( t ( H ) + c ) + 2 ( m ( H ) − c + 2 ) ) − ( t ( H ) + 2 m ( H ) = 4 − c ) \Delta \Phi\leqslant ((t(\mathcal H)+c)+2(m(\mathcal H)-c+2))-(t(\mathcal H)+2m(\mathcal H)=4-c) ΔΦ ⩽ (( t ( H ) + c ) + 2 ( m ( H ) − c + 2 )) − ( t ( H ) + 2 m ( H ) = 4 − c ) c i = O ( c ) c_i=\mathcal O(c) c i = O ( c )
则在考虑到势能可以随便修改单位1 1 1
c ^ i = O ( c ) + ( 4 − c ) k = O ( 1 ) \hat c_i=\mathcal O(c)+(4-c)k=\mathcal O(1) c ^ i = O ( c ) + ( 4 − c ) k = O ( 1 ) Delete# 只需要将对应节点调整到− ∞ -\infty − ∞
摊还O ( log n ) \mathcal O(\log n) O ( log n )
*Pairing heap# WARNING 想不清楚,咕掉了
重要定义
配对堆是一个带权多叉堆 配对堆是纯粹的树形结构,不额外维护信息
合并时直接把新来的插到左边
下面随着我们
删除是配对堆的核心操作
直接看代码
Node * merges (Node * x ) { if (x == nullptr || x->sibling == nullptr) return x; // 如果该树为空或他没有下一个兄弟,就不需要合并了,return。 Node * y = x->sibling; // y 为 x 的下一个兄弟 Node * c = y->sibling; // c 是再下一个兄弟 x->sibling = y->sibling = nullptr; // 拆散 return meld ( merges (c), meld (x, y)); // 核心部分 } 这里 meld(T1,T2)是配对操作
Decresed key
我们得进一步重构了
复杂度分析学# 均摊分析# 聚合分析# 账分析# 势分享# 主定理#