*课程框架树#

• Advanced DS
  • Search
    • AVL
    • RB
    • B+
    • [App]Inverted file index
  • heap
    • Leftist
    • Skew
    • Binomial
    • Fibonacci
    • Paring
• Algorithm
  • Design Technique
    • Basic
      • Greedy
      • DP
      • Devide and Conquer
      • Backtracking
    • Opti.
      • Approximation
      • Local search
    • misc
      • Randomized
      • *Parallel
      • External Sorting
  • Analysis Technique
    • PC vs NPC
    • Amortized Analysis

Backtracking#

补充定义

• $S_i$为$i$步的可选域
• game tree 又叫决策树

例一:八皇后

$$S_i\{1\cdots 8\}\\ x_i\neq x_j(i\neq j)\\ \left|\frac{(x_i-x_j)}{(i-j)}\right|\neq 1(i\neq j)$$

另外一个例子的阶段设计则没有那么显然

eg2. Turnpike Reconstruction

$$S_1=[1,n] \\S_{i-1} =S_i-\{l_i\}\vee S_{i-1}=S_i-\{r_i\}\\$$

每个阶段的决策并不好用变量来写

具体而言我们考虑用递归的方式定义这个过程

$\mathrm{Reconstruction}(X,D,N,l,r)$

表示我们已经将$[1,l-1],[r+1,N]$之间产生的距离全部从$D$中取出，你需要安排$X[l\to r]$的位置，能否产生可行解的过程

后续递归显然，剪枝即为，我们在选左和选右缩减时需要提前检查是否出现了未知的距离

Alpha-Beta prunning#

• Minmax Strategy:以tic-tac-toe为例，A与B分别持有最大化/，最小化某一收益的前提目标，则我们可以对game tree奇偶分层分别实现最值
• Alpha-Beta punning:基于该想法卡上下界（开始进入有奇偶两种），可以在实践中缩减规模到$\mathcal O(\sqrt N)$的效率($N$表示搜索树整体节点数)

Divide and Conquer#

Definition#

• Divide ：将问题规模切割成结构相似的子问题
• Conquer : 递归解决子问题
• Combine : 总问题的解决依赖子问题的结果，同时也需要合并

Closest Points Problem#

$n$个平面上的点，求最近点对

算法描述

• 按照$x$坐标将点集分成等大小的两部分
• 处理两侧的最近点对和跨点集的最近点对
• 假设两侧的结果为$\delta$，则我们考虑$[x_0-\delta,x_0+\delta]$内的点
  • 任意选取范围内一个点，则可更新区域变为$[x_0-\delta,x_0+\delta]\times [y_0,y_0-\delta]$
  • 可以证明最多只有6个不重合的点
    • 对左右分看看

则复杂度为$T(N)=2T(\frac{N}{2})+\mathcal O(N)=\mathcal O(N\log N)$

复杂度分析#

迭代求解法/递归树法#

$$T(N)=...=\underbrace{c N_{leaves}}_{conquer}+\underbrace{\sum_{node_i}^{non-leaf-nodes}f(N_{node_i})}_{combine}$$

以$T(N)=2T(N/2)+\mathcal O(N)$为例

$k \to \infty ,2^kT(\frac{N}{2^k})\to \mathcal O(N)$

这个基于$N_0\in [1,\sigma)$,$T(N_0)=\mathcal O( 1)$

补充例子

$$T(N)=3T(\frac{N}{4})+\Theta (N^2)$$

展开有

$$\begin{align*} T(N)&=\sum _{i=0}^{\log_4N-1}\left(\frac{3}{16}\right)^i cN^2+\Theta (N^{\log _43}) \\&<\sum_{i=0}^\infty \left(\frac{3}{16}\right)^icN^2+\Theta (N^{\log _4 3})\\&=\frac{cN^2}{1-\frac{3}{16}}+\Theta (N^{\log_4 3})=\mathcal O(N^2) \end{align*}$$

这个过程$a=3,b=4,f(n)=\Theta (n^2)$

代换法/归纳法#

上面这个你猜一下带入即可

Master Method#

Form1#

Form 1

对于形如$T(N)=aT(N/b)+f(N)$的递推式： 1.若$f(N)=O(N^{(\log_ba)-\varepsilon})$, for $\varepsilon>0$,那么$T(N)=\Theta(N^{\log_ba});$ 2.若$f(N)=\Theta(N^{\log_ba})$,那么$T(N)=\Theta(N^{\log_ba}\log N);$ 3.若$f(N)=\Omega(N^{(\log_ba)+\varepsilon})$, for $\varepsilon>0$且$af(\frac Nb)<cf(N)$, for $c<1$ and $\forall N>N_0$,那么$T(N)=\Theta(f(N))$ regularity condition

注意

• Merge sort
  • $a=b=2$,case2, $T(N)=\mathcal O(N\log N)$
• $a=b=2,f(N)=N\log ⁡N$；
  • $f(N)=N\log ⁡N$，虽然 $N\log ⁡N=\Theta(N^{log_⁡{2}2})$，但是 $N\log⁡ N\not=\Theta(N^{\log⁡_2 2−\epsilon})$，所以不适用于情况 3；
  • 具体来说，$\lim\limits_{⁡N\rightarrow\infty}\frac{N\log ⁡N}{N^{1+\epsilon}}=\lim\limits_{⁡N\rightarrow\infty}\frac{\log ⁡N}{N^\epsilon}=0\text{ for fixed }\epsilon>0$；
  • 这个例子体现出了 $\epsilon$ 的一定作用；

对于形如 $T(N)=aT(\frac{N}{b})+f(N)$ 的递推式，我们需要依次证明，此处我们使用递归树法进行证明。

Case 1

$$T(N)=\Theta(N^{\log_{b}a})+\sum\limits_{j=0}^{\log_{b}N-1}a^jf(\frac{N}{b^j})$$

​ 而我们有条件 $f(N)=O(N^{\log_{b}a−\epsilon}),\text{ for }\epsilon>0$，将它代入到上式中得到：

$$\begin{aligned} T(N)&=\Theta(N^{\log_{b}a})+\sum\limits_{j=0}^{\log_{b}N-1}a^jO((\frac{N}{b^j})^{\log_{b}a-\epsilon})\\ &=\Theta(N^{\log_{b}a})+O(N^{\log_{b}a−\epsilon}×\sum\limits_{j=0}^{\log_{b}N−1}(\frac{a}{b^{\log_{b}a−\epsilon}})^j)\\ &=\Theta(N^{\log_{b}a})+O(N^{\log_{b}a−\epsilon}×\sum\limits_{j=0}^{\log_{b}N−1}(b^\epsilon)^j)\\ &=\Theta(N^{\log_{b}a})+O(N^{\log_{b}a−\epsilon}×\frac{1×(1−(b^\epsilon)^{\log_{b}N})}{1−b^\epsilon})\\ &=\Theta(N^{\log_{b}a})+O(N^{\log_{b}a−\epsilon}×\frac{N^\epsilon-1}{b^\epsilon−1})\\ &=\Theta(N^{\log_{b}a})+O(N^{\log_{b}a−\epsilon}×N^\epsilon)\\ &=\Theta(N^{\log_{b}a})+O(N^{\log_{b}a})\\ &=\Theta(N^{\log_{b}a}) \end{aligned}$$

​ 证毕

Case 2

$$T(N)=\Theta(N^{\log_{b}a})+\sum\limits_{j=0}^{\log_{b}N-1}a^jf(\frac{N}{b^j})$$

而我们有条件 $f(N)=\Theta(N^{\log_{⁡b}a})$，将它代入到上式中得到：

$$\begin{aligned} T(N)&=\Theta(N^{\log_{⁡b}a})+\sum\limits_{j=0}^{\log⁡_{b}N−1}a^j\Theta((\frac{N}{b^j})^{\log⁡_{b}a})\\ &=\Theta(N^{\log_{⁡b}a})+\Theta(N^{\log_{b}a}×\sum\limits_{j=0}^{\log_{⁡b}N−1}(\frac{a}{b^{\log_{b}a}})^j)\\ &=\Theta(N^{\log_{⁡b}a})+\Theta(N^{\log_{b}a}×\log_{⁡b}N)\\ &=Θ(N^{\log_{⁡b}a}\log⁡N) \end{aligned}$$

证毕

Case 3

$$T(N)=\Theta(N^{\log_{b}a})+\sum\limits_{j=0}^{\log_{b}N-1}a^jf(\frac{N}{b^j})$$

接下来的步骤和之前不同。在继续之前，我们首先观察不等式 $af(\frac{N}{b})<cf(N)$，在我们的求和式中，我们观察到我们有大量的形如 $a^jf(\frac{N}{b^j})$ 的项，而这些项都可以通过迭代上面那个不等式来实现，即：

$$a^jf(\frac{N}{b^j})<c×a^{j−1}f(\frac{N}{b^{j−1}})<...<c^jf(N)$$

将这个不等式应用于求和式中，我们能够得到：

$$\begin{aligned} T(N)&<\Theta(N^{\log_{b}a})+\sum\limits_{j=0}^{\log_{b}N-1}c^jf(N)\\ &=\Theta(N^{\log_{b}a})+f(N)\sum\limits_{j=0}^{\log_{b}N-1}c^j\\ &=\Theta(N^{\log_{b}a})+f(N)\times\frac{1-c^{\log_{b}N}}{1-c}\\ &=\Theta(N^{\log_{b}a})+f(N)\times\frac{1-N^{\log_{b}c}}{1-c} \end{aligned}$$

而由于 $c<1$，所以 $\log_{⁡b}c<0$；而 $N>0$，而且一般非常大，所以 $N\log_{⁡b}c\in(0,1)$。因此，对于确定的常数 $c$，我们有 $\frac{1−N^{\log_{⁡b}c}}{1−c}\in(0,\frac{1}{1−c})$；

因此，上式便能改变为：

$$\begin{aligned} T(N)&<\Theta(N^{\log_{b}a})+f(N)\times\frac{1-N^{\log_{b}c}}{1-c}\\ &<\Theta(N^{\log_{b}a})+f(N)\times\frac{1}{1-c} \end{aligned}$$

并且，由于 $f(N)=\Omega(N^{\log_{⁡b}a+\epsilon}),\text{ for }\epsilon>0$，所以可以得到 $c_2N^{\log_{⁡b}a+\epsilon}<f(N)\Rightarrow N^{\log_{b}a}<\frac{1}{c_2N^\epsilon}f(N)$，因此 $T(N)<\Theta(N^{\log_{b}a})+f(N)\times\frac{1}{1-c}<c_1N^{\log_{b}a}+f(N)\times\frac{1}{1-c}<(\frac{c_1}{c_2N^\epsilon}+\frac{1}{1-c})f(N)=O(f(N))$

而我们知道，要证明 $T(N)=\Theta(f(N))$ 还需要证明 $T(N)=\Omega(f(N))$：

$$T(N)=Θ(N^{\log_{b}a})+\sum\limits_{j=0}^{\log_{b}N−1}a^jf(\frac{N}{b^j}) \geq\sum\limits_{j=0}^{\log_{b}N−1}a^jf(\frac{N}{b^j})\geq f(N)$$

由此得到 $T(N)=\Omega(f(N))$，最终证得 $T(N)=\Theta(f(N))$，至此证毕。

Form 2#

Form 2

对于形如 $T(N)=aT(\frac{N}{b})+f(N)$ 的递推式：

1. 若 $af(\frac{N}{b})=\kappa f(N)\text{ for fixed }\kappa <1$，那么 $T(N)=\Theta(f(N))$；
2. 若 $af(\frac{N}{b})=\kappa f(N)\text{ for fixed }\kappa >1$，那么 $T(N)=\Theta(N^{\log_{⁡b}a})=\Theta(a^{\log_{⁡b}N})$；
3. 若 $af(\frac{N}{b})=f(N)$，那么 $T(N)=\Theta(f(N)log_{⁡b}N)$；

对于形如 $T(N)=aT(\frac{N}{b})+f(N)$ 的递推式，基于线性关系的形式二的证明实际上和形式一的第三种情况的证明非常相像。

假设我们有 $af(\frac{N}{b})=cf(N)$，只需要讨论 c 的取值范围对结果的影响，就可以一次性得到结果。

类似于形式一的第三种情况的证明，我们迭代该关系式，得到关系：

于是，我们有：

我们现在并不像 Form 1 有显式的 $f(N)=\Omega(N^{\log_{⁡b}a+\epsilon})$ 的条件，而这个条件最终决定 conquer 部分和 combine 部分谁占主导地位。但是，我们实际上只需要得到 $f(N) = \Omega(N^{\log_{⁡b}a})$ 就够了。其实 $af(\frac{N}{b})∼cf(N)$ 这件事本身就暗含了它与 $N^{\log_{⁡b}a}$ 的关系：

可以发现，这一步还是和 Form 1 的第三种情况的证明过程高度相似。只不过现在我们要更进一步地看这个式子。

当 $c<1$ 时，实际上有 $f(N)>af(\frac{N}{b})$；当 $c=1$ 时，实际上有 $f(N)=af(\frac{N}{b})$；当 $c>1$ 时，实际上有 $f(N)<af(\frac{N}{b})$；

我们假设 $\frac{N}{b^L}$ 足够小（即递归到最末端，只需要进行 conquer 的时候），即 $\frac{N}{b^L}=\Theta(1)$，那么就有 $L=\Theta(\log_{⁡b}N)$。于是，我们有：

剩下的证明就跟 Form 1 的第三种情况一致

Form 3#

Form 3

当递推关系满足：

$$T(N)=aT(\frac{N}{b})+\Theta(N^k\log^{p}N)\text{ Where }a\geq 1,b>1,p\geq 0$$

其复杂度有结论：

$$T(N)= \begin{cases} O(N^{\log_{⁡b}a}),a>b^k\\ O(N^k\log⁡^{p+1}N),a=b^k\\ O(N^k\log^{p}N),a<b^k \end{cases}$$

Form4(re-Form3)#

(Chap4.5 4.1Master Method)

Form4

对于形如$T(N)=aT(N/b)+f(N)$的递推式： 1.若$f(N)=O(N^{(\log_ba)-\varepsilon})$, for $\varepsilon>0$,那么$T(N)=\Theta(N^{\log_ba});$ 2.若$f(N)=\Theta(N^{\log_ba}\log^k N)$,那么$T(N)=\Theta(N^{\log_ba}\log^{k+1} N);$ 3.若$f(N)=\Omega(N^{(\log_ba)+\varepsilon})$, for $\varepsilon>0$且$af(\frac Nb)<cf(N)$, for $c<1$ and $\forall N>N_0$,那么$T(N)=\Theta(f(N))$ regularity condition

实际上就是Form3的重述

Dynamic Programming#

Principle#

处理最优化问题，要求具有最优子结构。

例子#

Ordering Matrix Multiplications【Interval DP】#

题即其意

这里关于连乘方案，实际上就是画括号(卡特兰数)

$b_n=\frac{\binom{2n}{n}}{n+1}=\mathcal O(\frac{4^n}{n^{\frac{3}{2}}})$

Optimal Binary Search Tree【Interval DP】#

给定一些words 有$w_1<w_2<\cdots w_n$，每个有一个搜索概率$p_i$,你需要安排一个BST满足$w$约束，最小化

$$T(n)=\sum_{i=1}^n p_i(1+d_i)$$

假设$\mathcal T_{i,j}$表示$[i,j]$内的最优BST

$c_{i,j}$表示函数，$r_{i,j}$表示根，$w_{i,j}$是$\sum _{k=i}^j p_k$

这里相当于是考虑从哪里分开

Floyd#

设$f_k(i,j)$表示$i\to [l\leqslant k]\to j$的最短路

$f_{k}(i,j)=\min \{f_{k-1}(i,j),f_{k-1}(i,k)+f_{k-1}(k,j)\}$

注意到我们不需要存$k$

Greedy Algorithm#

Greedy Principle#

整体上

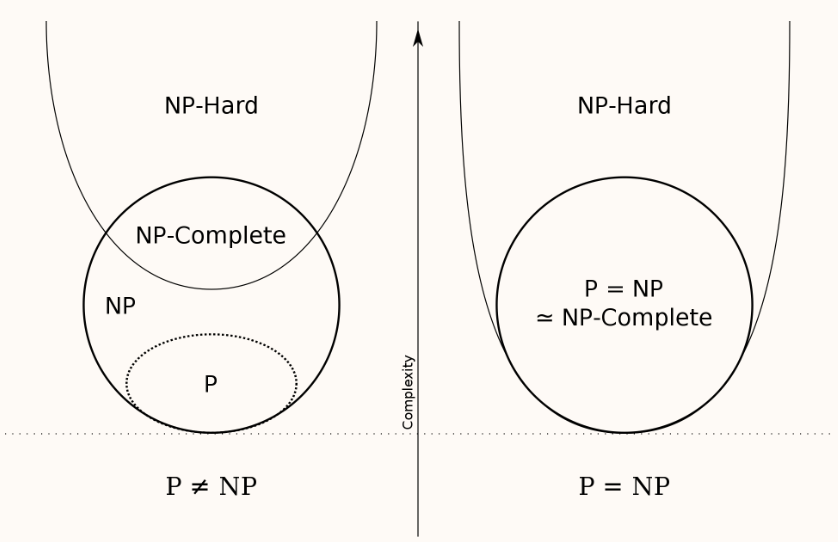
Huffman tree/code#

Np Completness#

这是一个

Concept#

• 图灵机

  • 图灵机由一个无限长的纸带和一个读写头组成。纸带被划分为一个个格子，每个格子上有一个符号，读写头可以在纸带上移动，读写头可以读取当前格子上的符号，也可以改变当前格子上的符号。图灵机的状态是一个有限集合，每个状态都有一个转移函数，转移函数的输入是当前状态和当前格子上的符号，输出是下一个状态、下一个格子上的符号和读写头的移动方向。

  • 确定型图灵机每次都能执行一个指令，并且根据当前指令跳转到下一个唯一的指令，非确定型图灵机可以从有限集中随意选择下一步，如果当前得到了一个答案，那么它一直都会选择正确的那一步。

• 多项式归约$\leq_P$ : $A\leq_P B \Leftrightarrow \exist f$，$f(A)=B,f^{-1}(B)=A$

• P（Polynomial Time）

• NP（Nondeterministic Polynomial Time）

  • 确定性图灵奖多项式验证
  • 不确定多项式多项式解决

• NPC

  • 是NP

  • $$B\in NP,\forall A\in NP,A\leq _P B\Rightarrow B\in NPC$$
  • $$B\in NP,A\in NPC,A\leq _P B\to B \in NPC$$

• NPH(NP Hard)

  • $$\forall A\in NP,A\leq_P B\Rightarrow B\in NPH$$

  • $NPC=NP\cap$​

  • NP-Hard 可以是NP，也可以不是NP

  

• Undecidable 不可判定

NPC#

第一个是Circuit-SAT->3-SAT

3SAT约束了布尔表达式的范式

NPH#

经典问题#

• Vertex Cover:选一个最小子集，覆盖所有边

• SAT:

  • 2-SAT是P的
  • 3-SAT (and , or , not)运算符

Approximation#

Approximation Ratio & Scheme#

$\rho =\max \left\{\frac{f_n(x)}{f_n(x^*)},\frac{f_n(x^*)}{f_n(x)}\right\}$

则称算法为 $\rho$-approx 算法

近似范式是对一个优化问题，一族相同模式的算法

满足$\rho\leqslant 1+\varepsilon,\varepsilon >0$

复杂度可以记为

• $$\mathcal O(n^{f(\varepsilon^{-1} )})$$

  成为多项式时间近似范式，Polynomial-time Approximation Scheme, PTAS）

• $$\mathcal O(n^{a}\varepsilon ^b)$$

​ 称为完全多项式时间近似范式**（Fully Polynomial-Time Approximation Scheme, FPTAS）**

在PTAS中,$\varepsilon$的变化是难以接受的

Examples#

Bin Packing#

n个$a_i\in(0,1]$，求最小分组方案，每个组和$\leqslant 1$

变种 $k$能否装$n$个$a_i$是一个NPC

Online Algorithm#

NF Next Fit#

NF策略总是选择最后一个组加

这里我们当然可以详细写，没必要

这里有一种构造让其取到2

如何让近似比更小？

First/Best Fit#

总是找第一个/最紧的bin

有1.7的界

最适合的垃圾箱包装 - 维基百科 --- Best-fit bin packing - Wikipedia

All in all#

具体来说，有以下定理：对于本题的所有近似算法，得到的近似解桶数至少是最优解桶数 $\frac{5}{3}$​ 倍。因此，我们需要采用离线算法来提升近似的准确度。

对手法

证明演示

我们作为对手和对面达成公式，你不能

我们首先构造$34$个

则此时你不能开

因为你开了就产生了$\rho \geqslant 2$

然后接着给你两个17

• 一个，给三个26
• 两个，给两个34

Offline#

FFD#

降序然后BF,

$\leqslant \frac{11}{9}M+\frac{6}{9}$

Knapsack#

Greedy PTAS#

• 性价比
• 买最大价值

结合起来

$AIG\geqslant \max\{x,y\},OPT=x+y$

我们可以设计

$y\leqslant \varepsilon OPT$

这里你可以取$1/\varepsilon$个东西，枚举其存在情况

DP FPTAS#

很容易写一个

但是注意，我们是关于

的多项式

这里有一种Round about的技术

K-center#

给一堆点，找K个，求最小K圆覆盖半径

注意这里距离是基于度量空间的

设$C=\{c_1,c_2,\cdots,c_k\}$为$k$个center,$S=\{s_1,\cdots,s_n\}$为$n$个site

$\text{minimize~} r(C) =\max _{s_i\in S}\{\min _{c_i\leqslant C} \{\text{dis}(s_i,c_i) \}\}$

Naive Greedy#

每次选能让下降最多的

Smarter#

说这个近似比是2

Themory:不可近似性#

K-center问题有没有$\rho<2$等价于$P=NP$

本质是找一个NPC,用一个$\rho<2$的方法归约他

具体而言是支配集

选定一个最小的子集，使得剩余点和这个子集中至少一个点相连

这是一个NPC问题

假设我们存在一个$\rho <2$​的方法$AlG$在$G'$工作

我们对于$G(V,E)$

构造$\mathrm{dis}(v,u)=\begin{cases}0&u=v\\1&u\to v\\ 2&u\not \to v \end{cases}$

r(C)=1已经找到。$r(C)>1\to r(C^*)>1$说明确实没有

这里具体的定义给了很多约束

这里可以换距离定义

Local Search#

整体刻画#

• $\mathcal L(S)$表示$S$的价值，我们需要$\operatorname{argmax}\mathcal L(S)$
• $S\to S'$​模式，每次对于一个状态找符合要求的邻集
• 👀 $\mathcal {FS}\to \bullet,\mathcal {FS}\xrightarrow{\text{small~}}$

GD - Climbing Algorithm#

这里实际上是假的梯度下降，每次我们选择邻集中的最值走

Vertex Cover Problem

这里我们构造$\mathcal L (S)\to |S|$

容易发现类似菊花图，线，完全二分图这种，假设你有一步没有删除对，则一定会导致不对

The Metropolis Algorithm#

我们随机选取邻集，假设更优就接受，假设不优

依赖$e^{-\frac{\Delta \mathcal L }{kT}}$来接受

IMPORTANT

Simulated Annealing

我们构造温度衰减

由于这里我们可能接受坏的结果，因此我们

Hopfield Neural Networks#

给图定黑白色，找有无方案使得 $\forall u\in S,\displaystyle \sum _{(u,v)\in E}w_es_us_v\leqslant 0$

• State-flipping Algorithm:
  • $S\to S'$,反转一个

可以证明$\mathcal T\leqslant \sum _{e}|w_e|$

Proof

$$\Phi (S)=\sum _{e,s_u\neq s_v} |w_e|$$

有

$$\Phi(S')=\Phi(S)-\sum _{e_u\mathtt {~is~bad}}|w_e|+\sum _{e_u\mathtt {~is~good}}|w_e|\geqslant \Phi(S)$$

有$0\leqslant \Phi(S)\leqslant W$

目标变成最大$\Phi$

直接做肯定不是多项式的

The Maximum Cut Problem#

给图定黑白色，最大化$\displaystyle \sum _{u\in A,v\in B}w_{uv}$

本质上是上一题$w\geqslant 0$的特例，然后直接套用算法

这里我们需要证明局部最优解有$2$的近似比

设最优解为$w(A^*,B^*)$