Reference & Analysis# 《Introduction to Modern Cryptography》
Introduction-to-modern-cryptography/现代密码学简介.pdf
Contest# >
Cheatsheet# 需要证明的部分我会用🙈标出来
期中all in one paper# *Intro of Crypto# 关于 Cryptography
kryptós /kryp.tós/ → /krypˈtos/ → /kripˈtos/ 表示 “hidden, secret”
把很多”不断加深的概念放在这里”
观念变化# Gen,Enc,Dec不可泄露->可泄露August Kerchoff 1884 密码系统只依赖密钥,方法可以公开 “攻击者不能获取额外信息”(关注某些位,长度这些额外信息) 从Shannon和Perfect认为攻击者无限强,后来都认为A \mathcal A A 从知识先于零知识到零知识脱离于知识Zero-Knowledge Proof, ZKP,陈述某种陈述的正确性,不泄漏任何陈述本身信息 协议中重要作用 传统密码学天才cracked game Caesar Cipher (Gen无随机性) Substitution Cipher 改成随机排列,那么我们引入 凯撒密码和变形
可用性P [ D e c ( E n c ( x ) ) = x ] = 1 \mathbb P[\mathrm{Dec}(\mathrm{Enc}(x))=x]=1 P [ Dec ( Enc ( x )) = x ] = 1 正确性 安全性 对我们关注的Provable Security
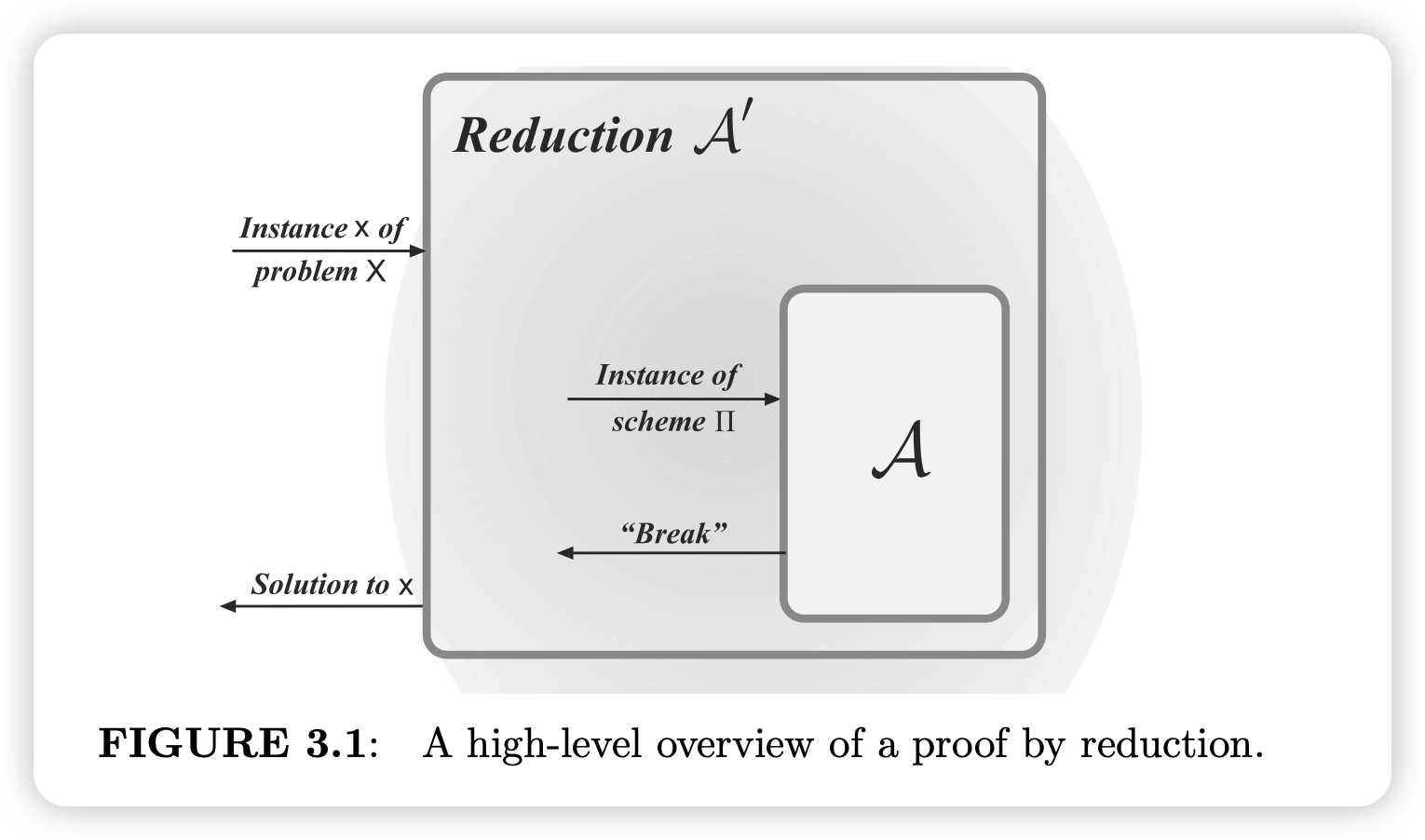
Precise Definition of Security Mathematic Assumpation Security Proof——Reduction Crypto Principles# 基础款加密系统定义
{ G e n , E n c , D e c , M , K } \{\mathrm{Gen,Enc,Dec,M,K}\} { Gen , Enc , Dec , M , K }
G E N ( s r a n d ) = s k \mathrm{GEN}(srand)=sk GEN ( sr an d ) = s k E N C ( s k , M ) = C \mathrm {ENC}(sk,M)=C ENC ( s k , M ) = C D E C O ( s k , C ) = D \mathrm{DECO}(sk,C)=D DECO ( s k , C ) = D Secure Multi-Party Computation # 计算一个关于秘密输入 x 1 , … , x n x_1, \dots, x_n x 1 , … , x n f f f f ( x 1 , … , x n ) f(x_1, \dots, x_n) f ( x 1 , … , x n ) π \pi π
正确性 (Correctness) :执行协议 π \pi π f ( x 1 , … , x n ) f(x_1, \dots, x_n) f ( x 1 , … , x n ) .完美的、诚实但好奇的 t -串通安全性 (t-security) :设 [ n ] [n] [ n ] { 1 , … , n } \{1, \dots, n\} { 1 , … , n } t t t 对于所有大小为 t 的集合 S ⊆ [ n ] S \subseteq [n] S ⊆ [ n ] Sim \text{Sim} Sim x 1 , … , x n x_1, \dots, x_n x 1 , … , x n
View S ( π ( x 1 , … , x n ) ) ≡ Sim ( x S , f ( x 1 , … , x n ) ) \text{View}_S(\pi(x_1, \dots, x_n)) \equiv \text{Sim}(x_S, f(x_1, \dots, x_n)) View S ( π ( x 1 , … , x n )) ≡ Sim ( x S , f ( x 1 , … , x n ))
其中,View S ( π ( x 1 , … , x n ) ) \text{View}_S(\pi(x_1, \dots, x_n)) View S ( π ( x 1 , … , x n )) i i i ∈ \in ∈ S S S
非诚勿扰的例子(?)
两个人出示0/1状态,如何设计协议使得两个人在诚信情况下 仅能获取是否同为1的结果(舔狗如何保护自己)
设计表格
然后按照 sa|1|sb 的方式连接成环
容易发现,只有11的情况是有长度为3的1连续段的
Shannon/Perfect Privacy# 介绍香农/完美安全互化,并陈述其局限性。本质是基于纯随机的等价概率分布的生成。
Shannon vs Perfect# 两个形式
Shannon ∀ t , c , P m ← D [ m = t ] = P m ← D , s k ← G e n [ m = t ∣ E n c ( s k , m ) = c ] \forall t,c,\mathbb P_{m\leftarrow D}[m=t]=\mathbb P_{m\leftarrow D,sk\leftarrow \mathrm{Gen}}[m=t\mid \mathrm{Enc}(sk,m)=c] ∀ t , c , P m ← D [ m = t ] = P m ← D , s k ← Gen [ m = t ∣ Enc ( s k , m ) = c ]
Perfect ∀ m 1 , m 2 , P s k ← G e n [ E n c ( s k , m 1 ) = c ] = P s k ← G e n [ E n c ( s k , m 2 ) = c ] ] \forall m_1,m_2,\mathbb P_{sk\leftarrow \mathrm{Gen}}[\mathrm{Enc}(sk,m1)=c]=\mathbb P_{sk\leftarrow \mathrm{Gen}}[\mathrm{Enc}(sk,m2)=c]] ∀ m 1 , m 2 , P s k ← Gen [ Enc ( s k , m 1 ) = c ] = P s k ← Gen [ Enc ( s k , m 2 ) = c ]]
Theorem
上述定义等价🙈
Hint:全概率展开
有一个推论
Shannon’s theorem
假设∣ M ∣ = ∣ K ∣ = ∣ C ∣ |M|=|K|=|C| ∣ M ∣ = ∣ K ∣ = ∣ C ∣ k k k E n c ( k , m ) = c \mathrm{Enc}(k,m)=c Enc ( k , m ) = c m , c m,c m , c k k k
One Time pad# M = { 0 , 1 } n = K G e n ( ⋅ ) → s k , s k ← $̸ K E n c ( s k , m ) = s k ⊕ m D e c ( s k , m ) = s k ⊕ c M=\{0,1\}^n=K\\\mathrm{Gen}(\cdot)\to sk,sk\xleftarrow {\not\$}K\\\mathrm{Enc}(sk,m)=sk\oplus m\\\mathrm{Dec}(sk,m)=sk\oplus c M = { 0 , 1 } n = K Gen ( ⋅ ) → s k , s k $ K Enc ( s k , m ) = s k ⊕ m Dec ( s k , m ) = s k ⊕ c 显然有P s k [ s k ⊕ m = c ] = P s k [ s k = m ⊕ c ] \mathbb P_{sk}[sk\oplus m=c]=\mathbb P_{sk}[sk=m\oplus c] P s k [ s k ⊕ m = c ] = P s k [ s k = m ⊕ c ]
OTP是Shannon-secure的
Theorem
香农安全必定有∣ K ∣ ⩾ ∣ M ∣ |K|\geqslant |M| ∣ K ∣ ⩾ ∣ M ∣
Hint:从映射不完全性出发
One-way function# Turing machine 假设
M \mathcal M M 图灵机 ,T ( M ) T(\mathcal M) T ( M ) ∀ x ∈ { 0 , 1 } ∗ \forall \mathbf x\in \{0,1\}^* ∀ x ∈ { 0 , 1 } ∗ M \mathcal M M T ( ∣ x ∣ ) T(|x|) T ( ∣ x ∣ )
A \mathcal A A
最后强调一下,n n n
eg
设P n \mathcal P_n P n P ∩ [ 2 n − 1 , 2 n − 1 ] \mathcal P \cap [2^{n-1},2^{n}-1] P ∩ [ 2 n − 1 , 2 n − 1 ] n n n
f : P n × P n → { 0 , 1 } 2 n f:\mathcal P_n\times \mathcal P_n\to \{0,1\}^{2n} f : P n × P n → { 0 , 1 } 2 n
由素数定理π ( n ) ≈ n ln n \pi(n)\approx\frac{n}{\ln n} π ( n ) ≈ l n n n
∣ P n ∣ = π ( 2 n ) ≈ 2 n n |\mathcal P_n|=\pi (2^n)\approx\frac{2^n}{n} ∣ P n ∣ = π ( 2 n ) ≈ n 2 n
∀ A r , P x , r [ A ( f ( x ) ) = t ∣ f ( x ) = f ( t ) ] = P ( p , q ) ← $ P n × P n [ A ( z ) = ( p ′ , q ′ ) ∣ p ′ q ′ = p q = z ] = P ( p , q ) ← $ P n × P n [ A ( z ) = p q ] = n e g l ( n ) \begin{align*} \forall \mathcal A^r,\mathbb P_{x,r}[\mathcal A(f(x))=t\mid f(x)=f(t)]&=\mathbb P_{(p,q)\xleftarrow{\$}\mathcal P_n\times \mathcal P_n}[\mathcal A (z)=(p',q')\mid p'q'=pq=z]\ \\&=\mathbb P_{(p,q)\xleftarrow{\$}\mathcal P_n\times \mathcal P_n}[\mathcal A (z)=pq]=\mathtt {negl}(n) \end{align*} ∀ A r , P x , r [ A ( f ( x )) = t ∣ f ( x ) = f ( t )] = P ( p , q ) $ P n × P n [ A ( z ) = ( p ′ , q ′ ) ∣ p ′ q ′ = pq = z ] = P ( p , q ) $ P n × P n [ A ( z ) = pq ] = negl ( n ) 也即大数分解的概率
这里张聪上课说错了,不能直接用素数密度定理直接说明这个OWF性质
换一个
g : { 0 , 1 } n × { 0 , 1 } n → { 0 , 1 } 2 n : g ( x , y ) = x y g:\mathcal \{0,1\}^n \times \{0,1\}^n\to \{0,1\}^{2n}:g(x,y)=xy g : { 0 , 1 } n × { 0 , 1 } n → { 0 , 1 } 2 n : g ( x , y ) = x y
这个显然就不是strong OWF
我们取P n × P n ⊆ { 0 , 1 } n × { 0 , 1 } n \mathcal P_n\times \mathcal P_n\subseteq \{0,1\}^n\times \{0,1\}^n P n × P n ⊆ { 0 , 1 } n × { 0 , 1 } n
P [ ( x , y ) ∈ P n × P n ] = ∣ P n ∣ 2 2 2 n ≈ 1 4 n 2 \mathbb P[(x,y)\in \mathcal P_n\times \mathcal P_n]=\frac{|\mathcal P_n|^2}{2^{2n}}\approx\frac{1}{4n^2} P [( x , y ) ∈ P n × P n ] = 2 2 n ∣ P n ∣ 2 ≈ 4 n 2 1
则
P ( p , q ) ← $ { 0 , 1 } n × { 0 , 1 } n [ A ( z ) = ( p ′ , q ′ ) ∣ p ′ q ′ = p q = z ] ⩽ 1 − 1 4 n 2 \mathbb P_{(p,q)\xleftarrow{\$}\{0,1\}^n\times \{0,1\}^n}[\mathcal A (z)=(p',q')\mid p'q'=pq=z]\leqslant 1-\frac{1}{4n^2} P ( p , q ) $ { 0 , 1 } n × { 0 , 1 } n [ A ( z ) = ( p ′ , q ′ ) ∣ p ′ q ′ = pq = z ] ⩽ 1 − 4 n 2 1 这里我跳步了
hc
给定一个函数 f f f hc : { 0 , 1 } ∗ → { 0 , 1 } \text{hc} : \{0,1\}^* \rightarrow \{0,1\} hc : { 0 , 1 } ∗ → { 0 , 1 }
可计算性 :
hc \text{hc} hc 可以在多项式时间内计算。
难以预测性 :对于任意概率多项式时间算法
A \mathcal A A ,存在一个可忽略函数
negl ( n ) \text{negl}(n) negl ( n ) ,使得
P x ← 0 , 1 n [ A ( 1 n , f ( x ) ) = hc ( x ) ] ≤ 1 2 + negl ( n ) \mathbb P_{x \leftarrow {0,1}^n} \left[ \mathcal A(1^n, f(x)) = \text{hc}(x) \right] \leq \frac{1}{2} + \text{negl}(n) P x ← 0 , 1 n [ A ( 1 n , f ( x )) = hc ( x ) ] ≤ 2 1 + negl ( n ) PRG# stream password
魔改OTP
G e n ( 1 n ) → s e e d ← $ { 0 , 1 } n E n c ( s e e d , m ) → s k ⊕ m D e c ( s e e d , c ) → s k ⊕ c \begin{align*}\mathrm{Gen}(1^n)&\to seed \overset{\$}{\leftarrow} \{0,1\}^n\\\mathrm{Enc}(seed,m)&\to sk\oplus m\\\mathrm{Dec}(seed,c)&\to sk\oplus c\end{align*} Gen ( 1 n ) Enc ( see d , m ) Dec ( see d , c ) → see d ← $ { 0 , 1 } n → s k ⊕ m → s k ⊕ c 这里需要一个混淆 seed和sk的东西
引入一个补充概念
EAV-secure/Semantic Security
∀ A r , i , P [ A ( 1 n , E n c ( s k , m ) ) = m i ] ⩽ 1 2 + n e g l ( n ) \forall \mathcal A^r,i,\mathbb P[\mathcal A(1^n,\mathrm{Enc}(sk,m))=m_i]\leqslant \frac{1}{2}+\mathtt {negl}(n) ∀ A r , i , P [ A ( 1 n , Enc ( s k , m )) = m i ] ⩽ 2 1 + negl ( n ) 实质上就是我们不能够通过对于加密结果的分析获取对于数据任意字段的信息
简单描述下PRG基于的游戏过程
c h → n , G e n , E n c , D e c A A → m 0 , m 1 , ∣ m 0 ∣ = ∣ m 1 ∣ c h c h → b ← { 0 , 1 } , s k ← G e n ( 1 n ) E n c ( s k , m b ) A A → b ′ c h ch\xrightarrow []{n,\mathrm {Gen,Enc,Dec}}\mathcal A\\ \mathcal A\xrightarrow {m_0,m_1,|m_0|=|m_1|}ch\\ ch\xrightarrow [b\leftarrow \{0,1\},sk\leftarrow \mathrm{Gen}(1^n )]{\mathrm{Enc(sk,m_b)}}\mathcal A\\ \mathcal A \xrightarrow {b'}ch c h n , Gen , Enc , Dec A A m 0 , m 1 , ∣ m 0 ∣ = ∣ m 1 ∣ c h c h Enc ( sk , m b ) b ← { 0 , 1 } , s k ← Gen ( 1 n ) A A b ′ c h 一句话就是A无法依赖ch给出的加密范式,区分自己提供的(也就是任意的)密文加密后的结果
给予一些额外的数学原理我们右
EVA-another definition
π = ( E n c , D e c ) \pi = (\mathrm{Enc},\mathrm{Dec}) π = ( Enc , Dec )
∀ A r , f : { 0 , 1 } n → { 0 , 1 } , D , ∃ A ′ ∣ P [ A ( 1 n , E n c ( s k , m ) ) = f ( m ) ] − A ′ ( 1 n ) = f ( m ) ∣ ⩽ n e g l ( n ) \forall \mathcal A^r,f:\{0,1\}^n\to \{0,1\},\mathcal D,\exist \mathcal A' \\\left|\mathbb P[\mathcal A(1^n,\mathrm{Enc}(sk,m))=f(m)]-\mathcal A'(1^n)=f(m)\right|\leqslant \mathtt {negl}(n) ∀ A r , f : { 0 , 1 } n → { 0 , 1 } , D , ∃ A ′ ∣ P [ A ( 1 n , Enc ( s k , m )) = f ( m )] − A ′ ( 1 n ) = f ( m ) ∣ ⩽ negl ( n ) 依赖上述过程我们可以给出PRG的标准定义
PRG def
设 G : 1 n → 1 l ( n ) G:1^n\to 1^{l(n)} G : 1 n → 1 l ( n ) D \mathcal D D A \mathcal A A
∀ A r : { 0 , 1 } l ( n ) → P P T { 0 , 1 } , ∣ Pr s ← { 0 , 1 } n , r ← G ( s ) [ A ( r ) = 1 ] − Pr r ← $ { 0 , 1 } l ( n ) [ A ( r ) = 1 ] ∣ ≤ n e g l ( n ) \forall \mathcal A^r:\{0,1\}^{l(n)}\xrightarrow{PPT} \{0,1\},\left|\Pr_{s \leftarrow \{0,1\}^n, r \leftarrow G(s)}[\mathcal A(r)=1]-\Pr_{r \xleftarrow{\$}\{0,1\}^{l(n)}}[\mathcal A(r)=1]\right| \leq \mathtt{negl}(n) ∀ A r : { 0 , 1 } l ( n ) PPT { 0 , 1 } , s ← { 0 , 1 } n , r ← G ( s ) Pr [ A ( r ) = 1 ] − r $ { 0 , 1 } l ( n ) Pr [ A ( r ) = 1 ] ≤ negl ( n ) 这里有一个外包任务,我们可以依赖EVA-secure的游戏形式构造reduction
在PRG中,我们往这个有些一半丢均匀分布,一般丢G ( x ) G(x) G ( x ) A ′ \mathcal A' A ′
PRG chain(hybrid argument)# 这里我们先给出尽量严谨的论述
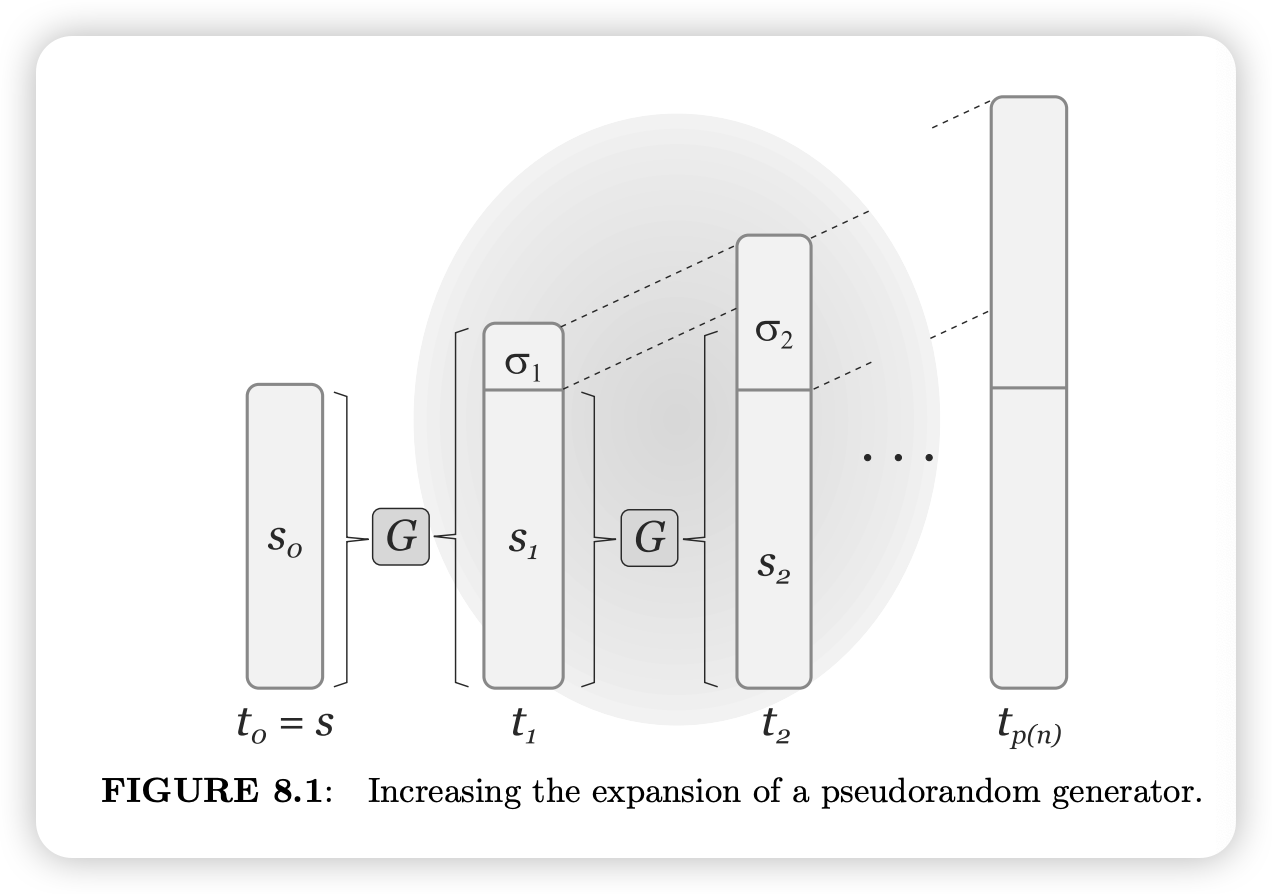
PRG可扩展定理
假设G : { 0 , 1 } n → { 0 , 1 } n + 1 G:\{0,1\}^n\to \{0,1\}^{n+1} G : { 0 , 1 } n → { 0 , 1 } n + 1 p o l y ( n ) \mathrm{poly}(n) poly ( n ) G ^ : { 0 , 1 } n → { 0 , 1 } p o l y ( n ) \hat G :\{0,1\}^n\to \{0,1\}^{\mathrm{poly(n)}} G ^ : { 0 , 1 } n → { 0 , 1 } poly ( n )
这里我不知道为什么老师要取p o l y ( n ) = 2 n \mathrm {poly}(n)=2n poly ( n ) = 2 n n n n
上述证明称为 hybrid argument 这里不做解释 (P282)
Multi-message-secure# 容易发现我们之前构造的流密码,缩短了sk但是还是只能一次一密,我们可以利用异或的可逆性构造冲撞,获取额外信息,考虑下面的游戏
c h M 0 , M 1 → G e n , E n c , D e c A c h E n c ( s k , M b ) ← ( M 0 , 1 ⋯ M 0 , k ) , ( M 1 , 1 ⋯ M 1 , k ) A c h ↔ b ′ { E n c ( M b , ∗ ) } A ch\overset{\overset{\mathrm{ Gen,Enc,Dec}}{\to } }{\tiny{M_0,M_1}}A\\\\ch\overset{\overset{(M_{0,1}\cdots M_{0,k}),(M_{1,1}\cdots M_{1,k})}{\leftarrow}}{\tiny \mathrm {Enc}(sk,M_b)} A\\ch\xleftrightarrow[b']{\{\mathrm{Enc}(M_{b,*})\}}\mathcal A c h M 0 , M 1 → Gen , Enc , Dec A c h Enc ( s k , M b ) ← ( M 0 , 1 ⋯ M 0 , k ) , ( M 1 , 1 ⋯ M 1 , k ) A c h { Enc ( M b , ∗ )} b ′ A 当我们提供来选择的消息为阵列时,情况有所不同
下面给出了一种方案
E n c ( s k , m , r ) → ( G ( s k ∣ ∣ r ) ⊕ M , r ) → ( c 1 , c 2 ) D e c ( s k , c 1 , c 2 ) → G ( s k ∣ ∣ c 2 ) ⊕ c 1 \mathrm{Enc}(sk,m,r)\to (G(sk||r)\oplus M,r)\to (c_1,c_2)\\ \mathrm{Dec}(sk,c_1,c_2)\to G(sk||c_2)\oplus c_1 Enc ( s k , m , r ) → ( G ( s k ∣∣ r ) ⊕ M , r ) → ( c 1 , c 2 ) Dec ( s k , c 1 , c 2 ) → G ( s k ∣∣ c 2 ) ⊕ c 1 在这个意义上,我们泄露了一部分s k ′ sk' s k ′
IND-CPA# IND-CPA :indistinguishabable chosen-plaintext-attacks
从这个出发
c h → G e n , E n c , D e c A ch\xrightarrow {\mathrm{Gen,Enc,Dec}}A\\ c h Gen , Enc , Dec A 然后执行多轮
c h ↔ E n c s k ( m i ) m i A ch\xleftrightarrow [\mathrm{Enc}_{sk}(m_i)]{m_i}A\\ c h m i Enc s k ( m i ) A 这记为Phase1
challaenge Phase(注意这种二择一的只有一次) c h ↔ E n c s k ( m b ∗ ) m 1 ∗ , m 2 ∗ A ch\xleftrightarrow [\mathrm{Enc}_{sk}(m^*_{b})]{m^*_{1},m_{2}^*}A\\ c h m 1 ∗ , m 2 ∗ Enc s k ( m b ∗ ) A c h ↔ E n c s k ( m i ) m i A ch\xleftrightarrow [\mathrm{Enc}_{sk}(m_i)]{m_i}A\\ c h m i Enc s k ( m i ) A 最后猜b ′ b' b ′
下面我们考虑说明IND-CPA与Multi-Msg-Secure 的关系
回顾Multi-Msg P r i v k A , I I m u l t ( n ) \mathsf {Privk}^{\mathrm{mult}}_{\mathcal A,\mathrm{II}} (n) Privk A , II mult ( n )
c h M 0 , M 1 → G e n , E n c , D e c A c h E n c ( s k , M b ) ← ( M 0 , 1 ⋯ M 0 , k ) , ( M 1 , 1 ⋯ M 1 , k ) A ch\overset{\overset{\mathrm{ Gen,Enc,Dec}}{\to } }{\tiny{M_0,M_1}}A\\\\ch\overset{\overset{(M_{0,1}\cdots M_{0,k}),(M_{1,1}\cdots M_{1,k})}{\leftarrow}}{\tiny \mathrm {Enc}(sk,M_b)} A c h M 0 , M 1 → Gen , Enc , Dec A c h Enc ( s k , M b ) ← ( M 0 , 1 ⋯ M 0 , k ) , ( M 1 , 1 ⋯ M 1 , k ) A 在本题中的IND-CPA范式实际上可以用更强形式表示 CPA2
CPA2→Multi-Msg S显然
每次都可以问m i , 0 / 1 m_{i,0/1} m i , 0/1 E n c ( m i , b ) \mathrm{Enc}(m_{i,b}) Enc ( m i , b )
换句话对这个CPA,其问题都形如
c h ↔ E n c s k ( m i , b ∗ ) m i , 1 ∗ , m i , 2 ∗ A ch\xleftrightarrow [\mathrm{Enc}_{sk}(m^*_{i,b})]{m^*_{i,1},m_{i,2}^*}A\\ c h m i , 1 ∗ , m i , 2 ∗ Enc s k ( m i , b ∗ ) A CPA2→CPA可以直接将二择一的问变成确定问,这个reduce是显然的
CPA→CPA2是构造一个hybrid argument
1个power怎么扩展
用CPA来勾连b=0到b=1
这里我感性的描述下这个Game set
Game0:
分别问,( m 10 , m 11 ) , ⋯ ( m i 0 , m i 1 ) (m_{10},m_{11}),\cdots(m_{i0},m_{i1}) ( m 10 , m 11 ) , ⋯ ( m i 0 , m i 1 ) b i = 0 b_i=0 b i = 0
Game1:
分别问,( m 10 , m 11 ) , ⋯ ( m i 0 , m i 1 ) (m_{10},m_{11}),\cdots(m_{i0},m_{i1}) ( m 10 , m 11 ) , ⋯ ( m i 0 , m i 1 ) b i = 0 b_i=0 b i = 0
Game2:
分别问,( m 10 , m 11 ) , ⋯ ( m i 0 , m i 1 ) (m_{10},m_{11}),\cdots(m_{i0},m_{i1}) ( m 10 , m 11 ) , ⋯ ( m i 0 , m i 1 ) b i = 0 b_i=0 b i = 0
…
一句话,你最后是希望区分全0和全1
上面G a m e i Game_i G am e i G a m e i + 1 Game_{i+1} G am e i + 1
PRFs# 对于
F = F ( { 0 , 1 } n , { 0 , 1 } n ) \mathcal F=F(\{0,1\}^n,\{0,1\}^n) F = F ({ 0 , 1 } n , { 0 , 1 } n ) 我们有∣ F ∣ = ( 2 n ) 2 n |\mathcal F|=(2^n)^{2^n} ∣ F ∣ = ( 2 n ) 2 n F I F_I F I
PRFs
F I \mathcal F_I F I I I I
ch首先把F I \mathcal F_I F I
然后ch自己在I I I b b b
然后A反复问m 1 m_1 m 1 b b b F s k ( m i ) F_{sk}(m_i) F s k ( m i ) y i y_i y i
P [ b = b ′ ] = 1 2 + n e g l ( n ) \mathbb P[b=b']=\frac{1}{2}+\mathtt{negl}(n) P [ b = b ′ ] = 2 1 + negl ( n )
更形式化
∣ P [ D ( F s k ( 1 n ) = 1 ) ] − P [ D ( f ( 1 n ) = 1 ) ] ∣ ⩽ n e g l ( n ) \left|\mathbb P[\mathcal D(F_{sk}(1^n)=1)]-\mathbb P[\mathcal D(f(1^n)=1)]\right|\leqslant \mathtt{negl}(n) ∣ P [ D ( F s k ( 1 n ) = 1 )] − P [ D ( f ( 1 n ) = 1 )] ∣ ⩽ negl ( n ) IND-CPA 2 PRFs# G e n ( 1 ′ ) → s k , { F } I E n c ( s k , m , r ) = ( r , F s k ( r ) ⊕ m ) D e c ( s k , c 1 , c 2 ) = c 2 ⊕ F s k ( r ) \mathrm{Gen}(1')\to sk,\{\mathcal F\}_I\\\mathrm{Enc}(sk,m,r)=(r,F_{sk}(r)\oplus m)\\\mathrm{Dec}(sk,c_1,c_2)=c_2\oplus F_{sk}(r) Gen ( 1 ′ ) → s k , { F } I Enc ( s k , m , r ) = ( r , F s k ( r ) ⊕ m ) Dec ( s k , c 1 , c 2 ) = c 2 ⊕ F s k ( r ) PRFs 2 IND-CPA# 对Reduction层面
ch给R F I \mathcal F_I F I s k sk s k
R基于定义生成G e n . E n c , D e c \mathrm{Gen.Enc,Dec} Gen.Enc , Dec
A丢回去m 1 m_1 m 1 r 1 r_1 r 1 s t r 1 str_1 s t r 1
然后R→( r 1 , s t r 1 ⊕ m 1 ) (r_1,str_1\oplus m_1) ( r 1 , s t r 1 ⊕ m 1 )
…
来A发出一次灵魂challenge
给m 0 ∗ , m 1 ∗ m_0^*,m_1^* m 0 ∗ , m 1 ∗
E n c ( m d ∗ ) \mathrm{Enc}(m_d^*) Enc ( m d ∗ ) b ′ = 0 / 1 b'=0/1 b ′ = 0/1 b b b
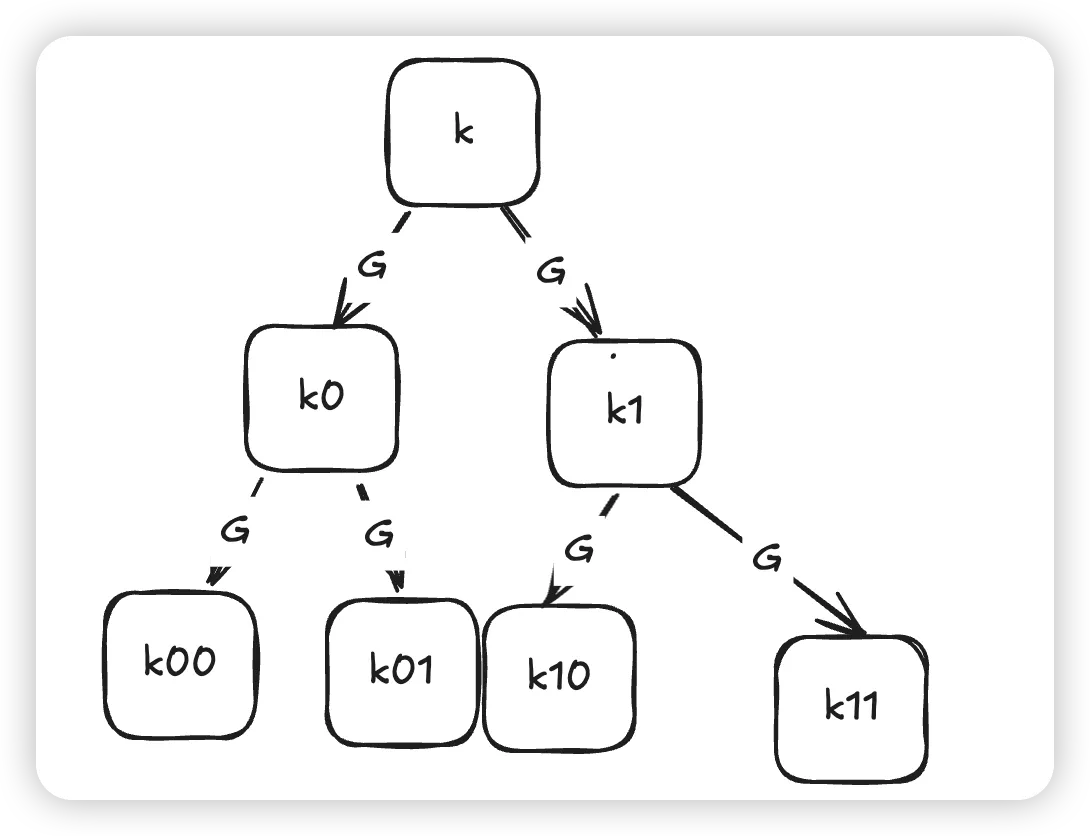
PRG 2 PRFs# 还是hybrid argument
相当于你需要从[ 0 , 2 n ) [0,2^n) [ 0 , 2 n ) 0 → [ 0 , 2 n ) 0→[0,2^n) 0 → [ 0 , 2 n )
首先我们假定G G G
Game0
Game1
Game1
…
这里一个问题是Game n-12 n − 1 2^{n-1} 2 n − 1
显然我们是求解具体一个O ( q ) \mathcal O(q) O ( q )
PRFs 2 PRG# 这个是显然的,一位一位即可
PRPs# PRPs
P I \mathcal P_I P I I I I
ch首先把P I \mathcal P_I P I
然后ch自己在I I I b b b
然后A反复问( m 0 , P ) (m_0,\mathcal P) ( m 0 , P ) ( m 1 , P − 1 ) (m_1,\mathcal P^{-1}) ( m 1 , P − 1 )
P [ b = b ′ ] = 1 2 + n e g l ( n ) \mathbb P[b=b']=\frac{1}{2}+\mathtt{negl}(n) P [ b = b ′ ] = 2 1 + negl ( n )
形式化定义如下
∣ P [ D ( P s k ( 1 n ) = 1 ) ] − P [ D ( π ( 1 n ) = 1 ) ] ∣ ⩽ n e g l ( n ) ∣ P [ D ( P s k − 1 ( 1 n ) = 1 ) ] − P [ D ( π − 1 ( 1 n ) = 1 ) ] ∣ ⩽ n e g l ( n ) \left|\mathbb P[\mathcal D(P_{sk}(1^n)=1)]-\mathbb P[\mathcal D(\pi(1^n)=1)]\right|\leqslant \mathtt{negl}(n)\\ \left|\mathbb P[\mathcal D(P^{-1}_{sk}(1^n)=1)]-\mathbb P[\mathcal D(\pi^{-1}(1^n)=1)]\right|\leqslant \mathtt{negl}(n) ∣ P [ D ( P s k ( 1 n ) = 1 )] − P [ D ( π ( 1 n ) = 1 )] ∣ ⩽ negl ( n ) P [ D ( P s k − 1 ( 1 n ) = 1 )] − P [ D ( π − 1 ( 1 n ) = 1 )] ⩽ negl ( n ) Cipher-Block-Chaining# E n c ( m , s k , r ) = ( r , F s k ⊕ m ) \mathrm {Enc}(m,sk,r)=(r,F_{sk}\oplus m) Enc ( m , s k , r ) = ( r , F s k ⊕ m ) 我们希望节省sk生成的开销
一个循环利用的想法应运而生
E n c ( s k , m 1 ∣ ∣ m 2 ∣ ∣ ⋯ m t , r ) = ( r , F s k ( r ) ⊕ m 1 , F s k ( c 1 ) ⊕ m 2 , ⋯ , F s k ( c t − 1 ) ⊕ m t ) \mathrm{Enc}(sk,m_1||m_2||\cdots m_t,r)=(r,F_{sk}(r)\oplus m_1,F_{sk}(c_1)\oplus m_2,\cdots,F_{sk}(c_{t-1})\oplus m_t) Enc ( s k , m 1 ∣∣ m 2 ∣∣ ⋯ m t , r ) = ( r , F s k ( r ) ⊕ m 1 , F s k ( c 1 ) ⊕ m 2 , ⋯ , F s k ( c t − 1 ) ⊕ m t ) 但显然这里F F F ( r , P k ( m , r ) ) ↔ m (r,P_k(m,r))\leftrightarrow m ( r , P k ( m , r )) ↔ m
MAC# 这部分我们暂时不看机密性,我们开始关注可信性
M A C ( s k , m ) → τ , ( m , τ ) \mathrm{MAC}(sk,m)\to \tau,(m,\tau) MAC ( s k , m ) → τ , ( m , τ ) 真实的数字签名没有sk
攻击者必须仿造( m ′ , τ ′ ) (m',\tau') ( m ′ , τ ′ )
unforgeability chosen message attack(UCMA)
UCMA模型的安全性通常与数字签名的存在性不可伪造性(Existential Unforgeability)相关联。如果一个数字签名方案在UCMA模型下是安全的,那么可以认为该方案具有EUF-CMA (Existential Unforgeability under Chosen Message Attacks)的安全性
整体思路是设计
{ G e n ( 1 n ) → s k M A C ( s k , m ) → τ V e r i f y ( s k , τ , m ) ∈ { 0 , 1 } \begin{cases}\mathrm{Gen}(1^n)\to sk\\\mathrm{MAC}(sk,m)\to \tau\\\mathrm{Verify}(sk,\tau,m)\in \{0,1\}\end{cases} ⎩ ⎨ ⎧ Gen ( 1 n ) → s k MAC ( s k , m ) → τ Verify ( s k , τ , m ) ∈ { 0 , 1 } c h → G e n , M A C , V e r i f y A c h ⇋ M A C s k ( m 1 ) / V e r i f y s k ( m 1 ) m 1 / ( m 1 , τ 1 ) A ⋯ c h ⇋ M A C s k ( m t ) m t A c h ← τ ∗ m ∗ A ch\xrightarrow {\mathrm{Gen,MAC,Verify}} \mathcal A\\ch\xleftrightharpoons[\mathrm{MAC}_{sk}(m_1)/\mathrm{Verify_{sk}}(m_1)]{\mathrm{m_1}/(m_1,\tau_1)} \mathcal A\\\cdots\\ch\xleftrightharpoons[\mathrm{MAC}_{sk}(m_t)]{\mathrm{m_t}} \mathcal A\\ch\xleftarrow[\tau^*]{\mathrm{m^*}} \mathcal A c h Gen , MAC , Verify A c h m 1 / ( m 1 , τ 1 ) MAC s k ( m 1 ) / Verif y sk ( m 1 ) A ⋯ c h m t MAC s k ( m t ) A c h m ∗ τ ∗ A P [ A w i n s ] = P [ V e r i f y ( m ∗ , τ ∗ ) = 1 ] = n e g l ( n ) \mathbb P[A~wins]=\mathbb P[\mathrm{Verify(m^*,\tau^*)}=1]=\mathtt{negl}(n) P [ A w in s ] = P [ Verify ( m ∗ , τ ∗ ) = 1 ] = negl ( n )
注意A \mathcal A A
密码学作业# 第一次作业 One Time Pad & OWF & PRG# 这一节作业没有更新勘误,因此看个大概就行,懒得改成提交的版本
Question 1: A Flawed One-Time Pad# Description
Consider a variant of the one-time pad with message space { 0 , 1 } n \{0, 1\}^n { 0 , 1 } n n n n n n n
Answer:
Let the key set be denoted by K K K ∣ K ∣ = ∑ i = 0 n − 1 ( n i ) = 2 n − 1 |K|=\sum _{i=0}^{n-1}\binom{n}{i}=2^{n-1} ∣ K ∣ = ∑ i = 0 n − 1 ( i n ) = 2 n − 1
For any m 1 m_1 m 1 m 2 m_2 m 2 n n n
Pr s k [ m 1 ⊕ s k = c ] = { 1 2 n − 1 if pop_count ( c ) ≢ 0 m o d 2 0 if pop_count ( c ) ≡ 0 m o d 2 \Pr_{sk}[m_1 \oplus sk = c] = \begin{cases} \frac{1}{2^{n-1}} & \text{if } \text{pop\_count}(c) \not\equiv 0 \mod 2\\ 0 & \text{if } \text{pop\_count}(c) \equiv 0 \mod 2 \end{cases} s k Pr [ m 1 ⊕ s k = c ] = { 2 n − 1 1 0 if pop_count ( c ) ≡ 0 mod 2 if pop_count ( c ) ≡ 0 mod 2 Similarly,
Pr s k [ m 2 ⊕ s k = c ] = { 1 2 n − 1 if pop_count ( c ) ≡ 0 m o d 2 0 if pop_count ( c ) ≢ 0 m o d 2 \Pr_{sk}[m_2 \oplus sk = c] = \begin{cases} \frac{1}{2^{n-1}} & \text{if } \text{pop\_count}(c) \equiv 0 \mod 2\\ 0 & \text{if } \text{pop\_count}(c) \not\equiv 0 \mod 2 \end{cases} s k Pr [ m 2 ⊕ s k = c ] = { 2 n − 1 1 0 if pop_count ( c ) ≡ 0 mod 2 if pop_count ( c ) ≡ 0 mod 2 Thus, an adversary can determine the parity (odd or even) of the number of 1’s in the original message by examining the ciphertext c c c
Idea:
The original One-Time Pad encryption and decryption processes are defined as follows:
M = { 0 , 1 } n = K Gen ( ⋅ ) → s k , s k ← $ K Enc ( s k , m ) = s k ⊕ m Dec ( s k , c ) = s k ⊕ c M = \{0,1\}^n = K \\ \text{Gen}(\cdot) \to sk, sk \overset{\$}{\leftarrow} K\\ \text{Enc}(sk, m) = sk \oplus m \\ \text{Dec}(sk, c) = sk \oplus c M = { 0 , 1 } n = K Gen ( ⋅ ) → s k , s k ← $ K Enc ( s k , m ) = s k ⊕ m Dec ( s k , c ) = s k ⊕ c Under the condition that s k sk s k m 1 m_1 m 1 m 2 m_2 m 2 c c c
Pr s k [ m 1 ⊕ s k = c ] = Pr s k [ m 2 ⊕ s k = c ] \Pr_{sk}[m_1 \oplus sk = c] = \Pr_{sk}[m_2 \oplus sk = c] s k Pr [ m 1 ⊕ s k = c ] = s k Pr [ m 2 ⊕ s k = c ] However, the modification to the definition of K K K
Pr s k [ m 1 ⊕ s k = c ] ≠ Pr s k [ m 2 ⊕ s k = c ] if pop_count ( m 1 ) ≢ pop_count ( m 2 ) m o d 2 \Pr_{sk}[m_1 \oplus sk = c] \neq \Pr_{sk}[m_2 \oplus sk = c] \text{ if } \text{pop\_count}(m_1) \not\equiv \text{pop\_count}(m_2) \mod 2 s k Pr [ m 1 ⊕ s k = c ] = s k Pr [ m 2 ⊕ s k = c ] if pop_count ( m 1 ) ≡ pop_count ( m 2 ) mod 2 Question 2: One Way Functions vs Pseudorandom Generators# 2.1# Description
Let G G G n n n 2 n 2n 2 n G G G
Solution:
The definition of a PRG is that for any algorithm A A A A A A G : { 0 , 1 } n → { 0 , 1 } l ( n ) G:\{0,1\}^n\to \{0,1\}^{l(n)} G : { 0 , 1 } n → { 0 , 1 } l ( n ) l ( n ) = 2 n l(n)=2n l ( n ) = 2 n
∣ Pr s ← { 0 , 1 } n , r ← G ( s ) [ A ( r ) = 1 ] − Pr r ← R { 0 , 1 } l ( n ) [ A ( r ) = 1 ] ∣ ≤ n e g l ( n ) |\Pr_{s \leftarrow \{0,1\}^n, r \leftarrow G(s)}[\mathcal A(r)=1]-\Pr_{r \xleftarrow{\mathbb{R}}\{0,1\}^{l(n)}}[\mathcal A(r)=1]| \leq \mathtt{negl}(n) ∣ s ← { 0 , 1 } n , r ← G ( s ) Pr [ A ( r ) = 1 ] − r R { 0 , 1 } l ( n ) Pr [ A ( r ) = 1 ] ∣ ≤ negl ( n ) If G G G A \mathcal A A G G G
Idea:
Assume G ∈ PRG [ { 0 , 1 } n → { 0 , 1 } 2 n ] G \in \text{PRG}[\{0,1\}^n \to \{0,1\}^{2n}] G ∈ PRG [{ 0 , 1 } n → { 0 , 1 } 2 n ] A 0 \mathcal A_0 A 0
Pr x [ f ( A 0 ( G ( x ) ) = G ( x ) ] ⩾ 1 poly ( n ) \Pr_{x}[f(\mathcal A_0(G(x))=G(x)] \geqslant \frac{1}{\text{poly}(n)} x Pr [ f ( A 0 ( G ( x )) = G ( x )] ⩾ poly ( n ) 1 (G G G f f f
In this scenario, consider
A ′ : { 0 , 1 } 2 n → { 0 , 1 } ∣ A ′ ( r ) = [ G ( A 0 ( r ) ) = r ] \mathcal A':\{0,1\}^{2n}\to \{0,1\} \mid \mathcal A'(r)=[G(\mathcal A_0(r))=r] A ′ : { 0 , 1 } 2 n → { 0 , 1 } ∣ A ′ ( r ) = [ G ( A 0 ( r )) = r ] Then,
Pr s ← { 0 , 1 } n , r ← G ( s ) [ A ′ ( r ) = 1 ] = Pr s ← { 0 , 1 } n [ G ( A 0 ( G ( s ) ) ) = G ( s ) ] ⩾ 1 poly ( n ) \Pr_{s \leftarrow \{0,1\}^n, r \leftarrow G(s)}[\mathcal A'(r)=1] = \Pr_{s\leftarrow \{0,1\}^n}[G(\mathcal A_0(G(s)))=G(s)] \geqslant \frac{1}{\text{poly}(n)} s ← { 0 , 1 } n , r ← G ( s ) Pr [ A ′ ( r ) = 1 ] = s ← { 0 , 1 } n Pr [ G ( A 0 ( G ( s ))) = G ( s )] ⩾ poly ( n ) 1 and
Pr r ← R { 0 , 1 } 2 n [ A ′ ( r ) = 1 ] ≤ Pr r ← R { 0 , 1 } 2 n [ ∃ s ∈ { 0 , 1 } n , G ( s ) = r ] = 2 n 2 2 n = 1 2 n \Pr_{r \xleftarrow{\mathbb{R}}\{0,1\}^{2n}}[\mathcal A'(r)=1] \leq \Pr_{r\xleftarrow{\mathbb R}\{0,1\}^{2n}}[\exists s\in \{0,1\}^n,G(s)=r] = \frac{2^n}{2^{2n}} = \frac{1}{2^n} r R { 0 , 1 } 2 n Pr [ A ′ ( r ) = 1 ] ≤ r R { 0 , 1 } 2 n Pr [ ∃ s ∈ { 0 , 1 } n , G ( s ) = r ] = 2 2 n 2 n = 2 n 1 Thus,
∣ Pr s ← { 0 , 1 } n , r ← G ( s ) [ A ′ ( r ) = 1 ] − Pr r ← R { 0 , 1 } 2 n [ A ′ ( r ) = 1 ] ∣ ≥ ∣ 1 poly ( n ) − 1 2 n ∣ ≥ 1 poly’ ( n ) \left|\Pr_{s \leftarrow \{0,1\}^n, r \leftarrow G(s)}[\mathcal A'(r)=1]-\Pr_{r \xleftarrow{\mathbb{R}}\{0,1\}^{2n}}[\mathcal A'(r)=1]\right| \geq \left|\frac{1}{\text{poly}(n)}-\frac{1}{2^n}\right| \geq \frac{1}{\text{poly'}(n)} s ← { 0 , 1 } n , r ← G ( s ) Pr [ A ′ ( r ) = 1 ] − r R { 0 , 1 } 2 n Pr [ A ′ ( r ) = 1 ] ≥ poly ( n ) 1 − 2 n 1 ≥ poly’ ( n ) 1 Since 1 poly’ ( n ) ≠ n e g l ( n ) \frac{1}{\text{poly'}(n)} \neq \mathtt{negl}(n) poly’ ( n ) 1 = negl ( n ) G G G
2.2# Description
Given that F F F G G G
G G G G G G Solution:
Directly provide the construction: Let
F : { 0 , 1 } n → { 0 , 1 } l ( n ) F:\{0,1\}^n\to \{0,1\}^{l(n)} F : { 0 , 1 } n → { 0 , 1 } l ( n ) Construct
G : { 0 , 1 } n → { 0 , 1 } l ( n ) + 1 ∣ G ( r ) = concat ( F ( r ) , { 1 } ) G:\{0,1\}^n\to \{0,1\}^{l(n)+1} \mid G(r)=\text{concat}(F(r),\{\mathtt{1}\}) G : { 0 , 1 } n → { 0 , 1 } l ( n ) + 1 ∣ G ( r ) = concat ( F ( r ) , { 1 }) Here, concat \text{concat} concat G G G 1 1 1 F F F
Proof for OWF:
Since F F F
∀ A : { 0 , 1 } l ( n ) → { 0 , 1 } n , Pr x ← R { 0 , 1 } n [ F ( A ( F ( x ) ) ) = F ( x ) ] ⩽ n e g l ( x ) \forall \mathcal A:\{0,1\}^{l(n)}\to \{0,1\}^n, \Pr_{x \xleftarrow{\mathbb R}{} \{0,1\}^{n} }[F(\mathcal A(F(x)))=F(x)] \leqslant \mathtt{negl}(x) ∀ A : { 0 , 1 } l ( n ) → { 0 , 1 } n , x R { 0 , 1 } n Pr [ F ( A ( F ( x ))) = F ( x )] ⩽ negl ( x ) If G G G A 0 : { 0 , 1 } l ( n ) + 1 → { 0 , 1 } n , poly ( ⋅ ) \mathcal A_0:\{0,1\}^{l(n)+1}\to \{0,1\}^n,\text{poly}(\cdot) A 0 : { 0 , 1 } l ( n ) + 1 → { 0 , 1 } n , poly ( ⋅ )
Pr x ← R { 0 , 1 } n [ G ( A 0 ( G ( x ) ) ) = G ( x ) ] ⩾ 1 poly ( n ) \Pr_{x \xleftarrow{\mathbb R}{} \{0,1\}^n}[G(\mathcal A_0(G(x)))=G(x)] \geqslant \frac{1}{\text{poly}(n)} x R { 0 , 1 } n Pr [ G ( A 0 ( G ( x ))) = G ( x )] ⩾ poly ( n ) 1 Then we construct A 0 ′ : 0 , 1 l ( n ) → 0 , 1 n ∣ A 0 ′ ( r ) = A 0 ( concat ( r , 1 ) ) \mathcal A'_0:{0,1}^{l(n)}\to {0,1}^{n} \mid \mathcal {A}'_0(r)=\mathcal A_0(\text{concat}(r,{\mathtt{1}})) A 0 ′ : 0 , 1 l ( n ) → 0 , 1 n ∣ A 0 ′ ( r ) = A 0 ( concat ( r , 1 ))
A 0 ′ \mathcal A_0' A 0 ′
Pr x ← R { 0 , 1 } n [ F ( A 0 ′ ( F ( x ) ) ) = F ( x ) ] ⩾ 1 poly ( n ) \Pr_{x \xleftarrow{\mathbb R}{} \{0,1\}^n}[F(\mathcal A_0'(F(x)))=F(x)] \geqslant \frac{1}{\text{poly}(n)} x R { 0 , 1 } n Pr [ F ( A 0 ′ ( F ( x ))) = F ( x )] ⩾ poly ( n ) 1 This contradicts the fact that F F F
Proof for not PRG:
Construct
A ′ ′ : { 0 , 1 } l ( n ) + 1 → { 0 , 1 } ∣ { 1 r l ( n ) + 1 = 1 0 r l ( n ) + 1 = 0 \mathcal A'':\{0,1\}^{l(n)+1}\to \{0,1\} \mid \begin{cases}1 & r_{l(n)+1}=1\\ 0 & r_{l(n)+1}=0\end{cases} A ′′ : { 0 , 1 } l ( n ) + 1 → { 0 , 1 } ∣ { 1 0 r l ( n ) + 1 = 1 r l ( n ) + 1 = 0 Then
∣ Pr s ← { 0 , 1 } n , r ← G ( s ) [ A ( r ) = 1 ] − Pr r ← R { 0 , 1 } l ( n ) + 1 [ A ( r ) = 1 ] ∣ = 1 − 1 2 = 1 2 |\Pr_{s \leftarrow \{0,1\}^n, r \leftarrow G(s)}[\mathcal A(r)=1]-\Pr_{r \xleftarrow{\mathbb{R}}\{0,1\}^{l(n)+1}}[\mathcal A(r)=1]| = 1-\frac{1}{2} = \frac{1}{2} ∣ s ← { 0 , 1 } n , r ← G ( s ) Pr [ A ( r ) = 1 ] − r R { 0 , 1 } l ( n ) + 1 Pr [ A ( r ) = 1 ] ∣ = 1 − 2 1 = 2 1 Clearly, this contradicts the requirement for the PRG definition of being negligible.
In summary, the constructed G G G
第二次作业:CCA-PRP# >